L’origen de la teoria té lloc en el càlcul simbòlic de Heaviside del final del segle XIX, el qual fou emprat sistemàticament pels físics i pels enginyers en la resolució de problemes teòrics d’electricitat. Posteriorment, l’any 1926, Dirac introduí la seva funció d (delta de Dirac) com a instrument de treball que ajuda en el tractament de problemes de mecànica quàntica. Paradoxalment, tant en el càlcul simbòlic com en els treballs de Dirac, malgrat que hom cometia una sèrie d’abusos de llenguatge i d’incorreccions matemàtiques, els resultats pràctics eren bons. No fou fins després del 1945 que Laurent Schwartz formalitzà la teoria com un cos de doctrina dins l’anàlisi funcional i li donà tot el rigor. Definí els espais vectorials topològics D de funcions infinitament derivables de suport compacte reals de ℝn amb la topologia de la convergència uniforme i anomenà distribucions els funcionals lineals continus sobre D, els quals funcionals organitzà amb una topologia adequada, en un espai de distribucions D’. Les funcions integrables f (x) actuen com a distribucions per mitjà de la fórmula
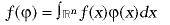
(si ϕ és de D), i això explica que les distribucions generalitzin el concepte de funció i el de mesura i aclareixin els abusos de llenguatge del càlcul simbòlic. La teoria de distribucions ha estat molt útil en la resolució de problemes de la teoria d’equacions diferencials en derivades parcials, que haurien estat insolubles amb el tractament clàssic de teoria de funcions.