A més, hom exigeix que l’operació × tingui la propietat distributiva respecte a la +. Hom pot dir, doncs, que un cos és un anell tal, que cada element té invers respecte a l’operació ×. Un cos té només dos ideals: el 0 i ell mateix. Els exemples més immediats són: el cos ℝdels nombres reals, amb les operacions usuals de suma i producte, el cos ℚdels nombres racionals i el ℂdels complexos. Hi ha el cos de dos elements 0 i 1, amb les operacions + (0 element neutre 1 + 1 = 0), i × habitual. Com a exemple de cos no commutatiu hi ha el dels quaternions. La característica d’un cos és el nombre més petit p, tal que 1 + 1 + ...p + 1 = 0; si no hi ha cap p> 0 amb aquesta propietat hom diu que el cos és de característica 0. Llevat d’aquest cas, la característica és sempre un nombre primer. Tot cos finit és commutatiu, de característica p = 0, i el nombre d’elements del cos és pn (recíprocament, per a tot p> 0 primer i tot n hi ha un cos de pn elements). La teoria de Galois estudia les extensions de cossos: un cos L que conté un subcos K és anomenat extensió de K, L és aleshores espai vectorial sobre K, i la seva dimensió és el grau de l’extensió. Un element de L que és arrel d’algun polinomi a coeficients en K, és anomenat algèbric sobre K, L és una extensió algèbrica de K si tots els elements de L són algèbrics sobre K (per exemple, el cos dels complexos és una extensió algèbrica de grau 2 dels reals). Donat un polinomi en K, hi ha una extensió en què el polinomi es descompon en factors lineals: és el cos de descomposició del polinomi. Si L és una extensió de K, el conjunt d’automorfismes de L que deixen fixos els elements de K és un grup. Si L és el cos de descomposició d’un polinomi p, aquest grup és anomenat grup de Galois de p, o també de l’extensió L. És un grup de permutacions d’arrels del polinomi. El teorema fonamental de la teoria estableix una bijecció entre els subgrups del grup de Galois de L sobre K els cossos intermedis entre L i K (continguts en L que contenen K). Per tant, el grup de Galois informa sobre el caràcter de l’extensió. En particular, si el grup és resoluble (grup), hi ha la possibilitat d’obtenir L adjuntant successivament a K “radicals", és a dir, arrels de polinomis del tipus xn-a. Això s’aplica al problema de resolució d’equacions algèbriques: per a les equacions de grau 2, 3 o 4 hi ha una fórmula que dóna l’expressió de les arrels (per exemple,
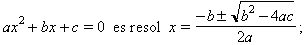
per a les equacions de grau 3 i 4 hi ha fórmules anàlogues, molt més llargues). Però per a equacions de grau 5 o més ja no hi cap expressió general d’aquest tipus, puix que hi ha polinomis que tenen com a grup de Galois el grup de permutacions de 5 elements, que no és resoluble, i, per tant, no serà possible de resoldre l’equació amb radicals. La teoria és aplicada també a l’estudi de les construccions geomètriques amb regle i compàs. Qualsevol problema de construcció d’aquest tipus pot ésser plantejat en termes algèbrics. Les dades són uns quants punts i corbes, que en un sistema de coordenades formen un conjunt de nombres reals que engendra un cert cos de nombres reals. Cada pas que hom fa amb regle i compàs construeix nous punts, i el cos engendrat és el mateix o una extensió quadràtica d’ell. Amb això hom demostra la impossibilitat de trisecció d’un angle, que correspondria a obtenir arrels d’un polinomi de tercer grau irreduïble, que mai no podia factoritzar en extensions de grau potències de 2. Tampoc no és possible de construir el cos tat d’un cub de volum 2 (si hom disposa del segment 1). I hom determina quins són els polígons regulars construïbles amb regle i compàs (per exemple, el de 7 costats no és possible).