El càlcul de probabilitats, branca de la matemàtica que presenta un gran nombre d’aplicacions científiques i tècniques, sorgí a França al s. XVII amb els matemàtics B. Pascal i P. Fermat. La motivació principal era l’estudi del guany esperat en els jocs d’atzar (ruletes, daus, cartes, etc. ) i, per tant, l’objectiu era el càlcul directe de la probabilitat utilitzant tècniques de combinatòria. La noció de probabilitat en què hom es basava fou formulada l’any 1795 pel matemàtic francès P. S. Laplace de la següent manera: “Si un fenomen pot produir un nombre de resultats diferents i igualment probables, la probabilitat d’un esdeveniment associat al fenomen és definida com el quocient del nombre de resultats favorables a l’esdeveniment pel nombre total de resultats possibles”. Un exemple familiar és la tirada d’un dau. Aquesta experiència dóna lloc a un conjunt de sis resultats possibles “obtenir un nombre superior a 4”, és 1/3. La descripció de Laplace, però, no pot ésser considerada com una definició matemàtica perquè no dóna un criteri que distingeixi els casos “igualment probables” dels que no ho són, i es tanca, doncs, en un cercle viciós. Això feia també que l’aplicació al càlcul generés diverses ambigüitats i paradoxes. Hom evita aquesta dificultat amb la llei empírica de l’atzar: “En una sèrie llarga de repeticions d’una experiència, la freqüència relativa d’un esdeveniment (quocient del nombre de vegades que es produeix pel nombre total de realitzacions) s’aproxima a la seva probabilitat”. La manca de precisió d’aquesta formulació la fa inadequada per als càlculs i no és tampoc un enunciat matemàtic perquè depèn de l’experimentació. En realitat constitueix una primera versió d’un dels resultats fonamentals de la teoria de la probabilitat, la llei dels grans nombres, demostrada en forma de convergència feble per J. Bernoulli l’any 1713. D’altra banda, l’estudi de les lleis de la probabilitat en els jocs d’atzar, sobretot en la situació d’experiències repetides, dóna l’explicació matemàtica de les regularitats estadístiques que es presenten en analitzar dades de poblacions molt nombroses. Per tal de constatar aquest fet fou necessari un coneixement profund de les lleis de la probabilitat, origen del desenvolupament de l’estadística matemàtica, que es proposa d’interpretar dades i resultats i extreure'n previsions per al futur. Els fenòmens anomenats aleatoris o estocàstics, com els jocs d’atzar, constitueixen el camp d’objectes de la probabilitat. Un primer intent de formular una axiomàtica de la teoria de la probabilitat es troba en els treballs de Richard von Mises (1928) i parteix de la regularitat estadística que presenten aquests fenòmens. Però fou el matemàtic rus A. N. Kolmogorov qui resolgué definitivament, el 1913, el problema de donar una base matemàtica a la probabilitat. Els elements que té en compte l’axiomàtica de Kolmogorov són, en primer lloc, que el caràcter aleatori d’un fenomen és degut a la manca de coneixença de totes les condicions físiques en què es produeix, i per això dóna lloc a un cert nombre de diferents resultats possibles, i la regularitat estadística de les repeticions no és, per tant, l’element bàsic, sinó una conseqüència del fet que el fenomen es realitzi sempre sota les mateixes condicions; i, en segon lloc, que els esdeveniments lligats a un fenomen aleatori són representats per subconjunts de resultats, de manera que l’esdeveniment impossible i l’esdeveniment segur corresponen, per exemple, al conjunt buit i al total, respectivament, i tot conjunt de resultats que correspon a un esdeveniment és anomenat observable. Aleshores, un espai de probabilitat (Ω, Q, P) dóna un model matemàtic per a descriure els fenòmens aleatoris, i consta, per definició, d’un conjunt Ω de resultats, d’una σ-àlgebra Q de conjunts observables o esdeveniments (família de subconjunts de Ω tancada per complementació, reunió numerable i que conté el buit) i d’una probabilitat P, la qual és una aplicació P:Q →[0, 1] que assigna a cada esdeveniment un nombre comprès entre 0 i 1, amb les propietats: P(Ω) = 1 i si (Ai ) i ∈ℕ és una família d’esdeveniments disjunts dos a dos, aleshores
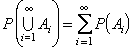
(propietats d’additivitat). En particular es compleix P(A ∪B) = P(A) + P(B) si A ∩B = ∅. Aquests axiomes no determinen el valor de la probabilitat, aspecte que correspon a l’aplicació d’aquesta teoria. Si Ω és finit, Q = P(Ω), i hom suposa que cada resultat o esdeveniment elemental té la mateixa probabilitat, la descripció de Laplace és un teorema que dóna la probabilitat de tot esdeveniment a partir de l’axioma d’additivitat. Sintàcticament, la probabilitat, juntament amb el volum, la longitud, el pes, la massa, etc. , forma part d’una teoria abstracta de la mesura. Cal assenyalar, però, dos aspectes que són específicament probabilístics: els conceptes de probabilitat condicionada i independència i l’estudi de les probabilitats sobre la recta real condicionada per un altre B representa una modificació de la probabilitat d'A per la informació que B s’ha produït i hom la defineix per P(A/B) = P(A ∩B)/P(B) si P(B) = 0. Aleshores hom diu que A i B són independents si P(A/B) = P(A), o, de manera equivalent, si P(A ∩B) = P(A) P(B). Aquesta noció d’independència és bàsica en l’estudi de les proves repetides. En tirar dues vegades consecutives un dau, el nombre de resultats és 36, i per exemple, els esdeveniments A = {treure un 2 a la primera tirada} i B = {treure un 3 a la segona tirada} són independents perquè P(A ∩B) = 1/36 = P(A) P(B). En el segon aspecte, les interpretacions numèriques d’un experiment aleatori (apostes en els jocs d’atzar, mesures, etc. ) donen lloc a la noció de variable aleatòria com una aplicació de ς en ℝque indueix aleshores una probabilitat en ℝanomenada llei de X. A part les lleis discretes obtingudes quan ς és finit o numerable, l’exemple més important de llei de probabilitat és la llei normal definida per
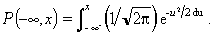
Aquesta llei fou estudiada pels matemàtics P. S. Laplace i C. F. Gauss en relació amb el càlcul d’errors, i l’any 1812 el matemàtic francès A. De Moivre demostrà que pot ésser obtinguda com a límit de lleis discretes. Aquest és el resultat fonamental de la teoria de la probabilitat, conegut amb el nom de teorema del límit central. La teoria de la probabilitat ha influït en molt diverses branques de la matemàtica, com la teoria de la informació i la teoria del potencial. D’altra banda, ha evolucionat cap a temes més específics, com els processos estocàstics, definits com a variables aleatòries que són funció del temps i introduïts en l’estudi de l’evolució de sistemes (econòmics, biològics i tècnics). Un dels primers exemples de procés estocàstic és el moviment brownià, del qual N. Wiener donà, el 1923, una descripció matemàtica precisa partint de les idees dels físics L. Boltzmann, sobre teoria ergòdica, i J. W. Gibbs, sobre l’estadística dels gasos. Diferents graus d’influència del passat damunt del present donen lloc a diferents tipus de processos, com els processos amb increments independents (cas del moviment brownià), les cadenes i els processos de Markov. Aquest desenvolupament comporta actualment l’ús de recursos d’anàlisi funcional per part de la teoria de la probabilitat, fet que no és nou, puix que al llarg del s. XIX els probabilistes ja utilitzaven elements d’anàlisi matemàtica, com les transformacions de Laplace i de Fourier, la teoria de distribucions i sobretot la integració de Lebesgue i de Stieltjes.