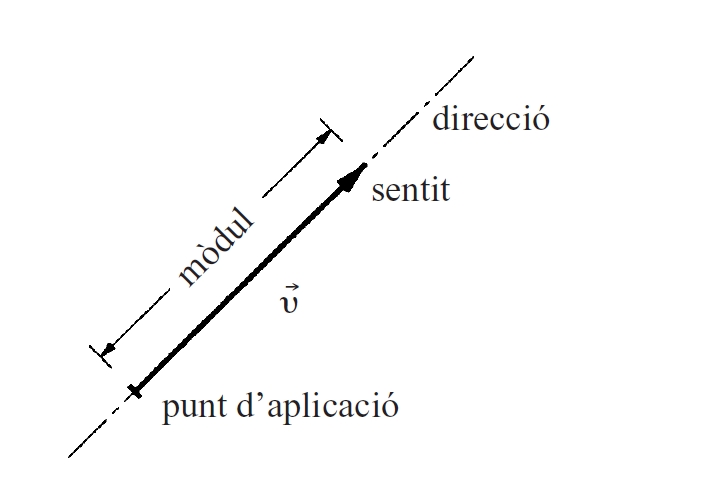
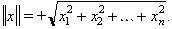Des del punt de vista geomètric, a tot vector se li pot associar direcció, mòdul i sentit, i un punt d’aplicació. Segons les seves posicions relatives, es parla de vectors simètrics, oposats, conjugats, ortogonals, etc.
Fixada una base de vectors e1,...,en en un espai vectorial E de dimensió n (base d’un espai vectorial), tot vector x de E pot ésser expressat en forma única com a combinació lineal dels elements de la base: x = x1e1 + ...+ xnen. Així, x resta determinat pels nombres x1,x2,...,xn, els quals són dits components de x; hom ho escriu x = (x1,...,xn). Si en E hom defineix un producte escalar (i en particular la noció de distància i d’angle) mitjançant x·y = x1y1 + x2y2 + ... + xnyn, aleshores les components resulten ésser les projeccions ortogonals del vector sobre els eixos de referència.
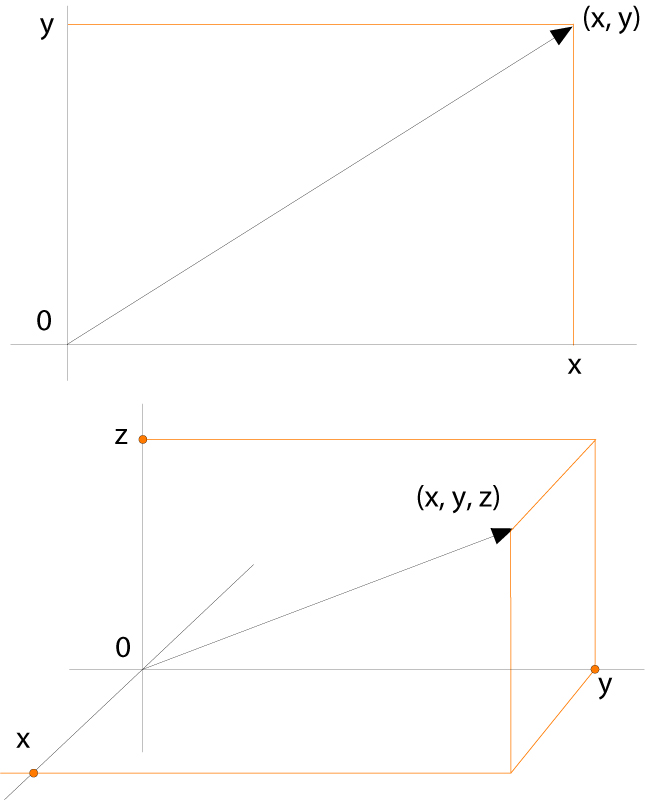
Vector fix del pla (a dalt) i de l’espai (a baix)
© Fototeca.cat