L’aplicació compleix que la mesura de la unió de dos conjunts A i B de ɑés igual a la suma de les respectives mesures, és a dir ∀ A ∈ɑi ∀ B ∈ɑtals que A ∩ B = ∅, m ( A ) + m ( B ). La terna (Ω, ɑ, m ) és anomenada espai de mesura , i els conjunts de l’àlgebra ɑsón anomenats mesurables . En el cas que ɑsigui una σ-àlgebra de Borel, una mesura m és anomenada σ-additiva si la mesura d’una unió infinita i numerable de conjunts de ɑdisjunts dos a dos és igual a la suma de les respectives mesures, és a dir
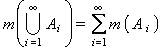
essent A i ∈ɑi A i ∩ A j = ∅, per a tot i, j tals que i ≠ j . Una mesura és anomenada fitada si, per a qualsevol A ∈ɑ, m ( A ) és menor o bé igual a un cert nombre real positiu. És important el cas en què Ω és la recta real ℝ, ɑés la mínima àlgebra de ℝque conté tots els intervals fitats ( a , b ) i m és l’anomenada mesura de Lebesgue , que assigna a cada interval ( a , b ) la longitud de l’interval, és a dir, m ( a,b ) — b — a. Cal dir, finalment, que una mesura que assigna el valor 1 al conjunt Ω és anomenada probabilitat . La teoria de la mesura , branca fonamental de l’anàlisi matemàtica, té el seu punt de partida en els problemes del càlcul de longituds, àrees i volums, com també en els d’integració de funcions. Els grecs (Èudox de Cnidos, Arquimedes, etc) foren uns dels primers a calcular mesures de figures concretes suposant que aquestes mesures existien sempre i que eren calculables a partir de mesures geomètriques elementals de figures simples (per exemple, la descomposició de polígons en triangles), és a dir, fent sempre una aproximació per excés de la mesura cercada a partir de mesures conegudes. Aquest tipus de problemes pràctics, juntament amb d’altres de caire físic, portaren a l’estudi de la integració de funcions, cosa que posà en evidència la necessitat d’estudiar els conjunts que admetessin una mesura i sobre els quals hom pogués calcular la integral de funcions que hi són definides. Cantor (1883), Stolz (1884) i Harnack (1885) donaren les primeres definicions generals de mesures de conjunts. Stolz i Harnack mesuraren conjunts afitats de la recta real i Cauchy obtingué la mesura d’un conjunt de ℝ 3 (o ℝ 2 ) com a límit dels volums (o àrees) de les esferes (o cercles) que contenen el conjunt, continuant així la tradició de calcular per excés. El fet de mirar l’additivitat finita, és a dir, descompondre un conjunt en trossos disjunts i considerar que la mesura del conjunt és la suma de les mesures de cada tros, és una idea formalitzada per Peano i Jordan. Per exemple, un conjunt A del pla ℝ 2 inclòs en un rectangle I és quadriculat, i hom troba la suma de les àrees dels rectangles de I inclosos en A i la suma de les àrees dels rectangles de la quadrícula de I que tenen almenys un punt en comú amb A ; així, refinant la quadriculació, hom arriba a una mesura per defecte i a una mesura per excés que, en cas de coincidir, donen la mesura cercada del conjunt. Borel i Fréchet consideraren la possibilitat de l’additivitat infinita, és a dir, dividir un conjunt en un nombre infinit i numerable de trossos i obtenir aleshores la mesura com una sèrie numèrica de les mesures de cada tros. Tot això menà Lebesgue, l’any 1902, a donar una definició general de mesura en el cas de ℝ n i considerar les funcions mesurables envers la integració. A partir de Lebesgue hom ha introduït noves mesures d’un nivell conceptual molt elaborat i abstracte (Carathéodory, Hahn, Stieltjes, Radon, Haar, Ulam, Bourbaki, etc). El tractament correcte dels espais de mesura, gràcies a la contribució de Radon i Nikodyn, fou l’instrument adequat per a tractar de la descripció dels fenòmens aleatoris, i fou Kolmogorov qui formulà l’axiomàtica bàsica de la teoria de la probabilitat com a cas particular de la teoria de la mesura (integral).