El so és generat sempre a partir de la vibració d’un sistema mecànic o acústic (cordes, membranes, columnes d’aire), que es propaga després a altres sistemes (caixes de ressonància, aire circumdant). La propagació d’aquesta vibració inicial s’anomena ona. Així doncs, la física del so s’ocupa bàsicament d’estudiar i formular de manera general el problema vibratori i ondulatori (descripció i anàlisi de vibracions, definició de les magnituds característiques, interacció entre sistemes vibratoris, fenòmens de propagació, etc.).
Vibracions
Reflexió i transmissió
© Fototeca.cat/ Studi Ferrer
Una vibració és qualsevol tipus de fluctuació que es produeix al voltant d’un valor mitjà (oscil·lador). Quan la fluctuació és d’una magnitud associada a un sistema o medi material, es parla de vibració mecànica o acústica, i el valor mitjà s’anomena valor d’equilibri i coincideix amb el valor d’aquesta magnitud quan el medi es troba en repòs. Quan un medi vibra, no solament fluctuen les magnituds que descriuen el moviment (posició, velocitat, acceleració), sinó també totes les altres que es relacionen amb les propietats del medi. Així, per al cas de les vibracions de l’aire, és freqüent parlar de les fluctuacions de la pressió i de la densitat. Per tal que aquest tipus de moviment sigui possible, cal que el sistema estigui sotmès a una força recuperadora que l’empenyi cap a l’equilibri cada vegada que se n’allunya. L’exemple paradigmàtic de sistema vibratori senzill és el d’un bloc suspès del sostre mitjançant una molla. En aquest cas, la molla proporciona la força de recuperació necessària.
Classificació de les vibracions
Tot problema vibratori comença amb una actuació externa al sistema que el posa en moviment. Segons el tipus d’actuació, les vibracions es poden classificar en quatre grups. Si l’actuació és instantània, es parla de vibració lliure. Si és mantinguda al llarg del temps, vibratòria i no influïda per la resposta del sistema, es tracta d’una vibració forçada. Si, en canvi, la resposta del sistema interacciona amb l’actuació externa i la modifica, llavors és una vibració acoblada. Finalment, si és mantinguda al llarg del temps però no és vibratòria sinó constant, es parla de vibració autoexcitada. Un exemple de vibració lliure és la d’una corda de piano sota l’acció instantània del martell (instruments de règim lliure). És una vibració forçada la d’un altaveu d’un equip de so, on la força mecànica que el fa bellugar prové d’un senyal elèctric amplificat que manté les seves característiques independentment del moviment de l’altaveu. Una vibració acoblada és la de la caixa d’un violí sota l’actuació (externa a la caixa) associada al moviment vibratori de la corda que recolza sobre el pont. En aquest cas, el moviment de la corda es veu condicionat pel moviment de la caixa. Un exemple de vibració autoexcitada és la de la columna d’aire continguda en un instrument de vent sota l’acció del cabal d’aire constant injectat pel músic, o la d’una corda de violí sota l’acció associada al moviment no vibratori de l’arquet (instruments de règim autoexcitat).
Les característiques d’aquests quatre tipus de vibracions són molt diferents. En el cas de les vibracions lliures, depenen exclusivament de les propietats del medi. Si es tracta de vibracions forçades, són imposades per l’agent. En el cas de les vibracions acoblades, depenen tant de les característiques de l’agent com de les del sistema. Si són autoexcitades, és bàsicament el sistema el que imposa les característiques de la vibració.
D’altra banda, l’existència ineludible de mecanismes de dissipació és responsable de l’extinció de les vibracions lliures a curt o llarg terminis (en funció de la intensitat de la dissipació), mentre que en el cas dels altres tipus de vibracions les dissipacions poden ser compensades per l’actuació exterior.
D’acord amb un criteri matemàtic, les vibracions es poden classificar en simples i complexes. Una vibració simple és la que correspon exactament al tipus d’oscil·lació que fa el sistema bloc-molla. Una vibració complexa és la que resulta de la superposició de diverses vibracions simples.
Magnituds associades a les vibracions
Des del punt de vista matemàtic i negligint l’existència de dissipacions, totes les magnituds associades a la vibració lliure del sistema bàsic bloc-molla (posició, velocitat o acceleració del bloc, o bé tensió de la molla) varien d’acord amb una llei sinusoidal que es caracteritza per la seva freqüència (o període) i per la seva amplitud. La freqüència és el nombre d’oscil·lacions idèntiques que realitza per segon i es mesura en hertz, mentre que el període, el seu invers, és el nombre de segons que triga el sistema a fer una oscil·lació completa. L’amplitud és el valor màxim que assoleix la magnitud vibratòria en una oscil·lació. Si es tenen en compte els efectes dissipatius, l’amplitud decreix a cada oscil·lació.
Quan es tracta d’una vibració simple lliure, la freqüència i el ritme d’extinció depenen exclusivament de les característiques del sistema, però l’amplitud depèn de la intensitat de l’actuació externa. Així, un cop de martell suau en una corda de piano dona lloc a un moviment de petita amplitud, mentre que un cop fort origina un moviment de gran amplitud. En tots dos casos, però, la freqüència de l’oscil·lació és la mateixa.
Les vibracions complexes, en canvi, no són sempre repetitives (o periòdiques), i per tant no se’ls pot associar de manera immediata una freqüència. Si són repetitives, llavors es pot parlar de freqüència o de període fonamental. En qualsevol cas, independentment del caràcter repetitiu o no, aquest tipus d’oscil·lació admet una anàlisi freqüencial, gràcies a la teoria desenvolupada al final del segle XVIII i el començament del XIX pel físic francès Jean Baptiste Fourier (1768-1830).
Anàlisi de Fourier
L’anàlisi de Fourier és la part de les matemàtiques que s’ocupa de l’estudi de les vibracions complexes. La idea bàsica que hi ha al darrere d’aquesta anàlisi és la descripció d’aquestes vibracions a partir de les vibracions simples. Fourier, que desenvolupà aquest tema en un llibre dedicat a la teoria de la calor, postulà que qualsevol vibració podia ser construïda a partir d’una sèrie de vibracions simples (i, per tant, de freqüència ben definida). El camí invers també era possible: qualsevol vibració podia ser descomposta en sèrie de vibracions simples. La descripció de les amplituds i freqüències d’aquest conjunt de vibracions simples que formen la vibració complexa s’anomena espectre de Fourier.
Quan la vibració complexa que s’estudia és periòdica, totes les freqüències de l’espectre són necessàriament múltiples enters o harmònics de la freqüència de la vibració original, que s’anomena freqüència fonamental (sèrie delsharmònics). Si es tracta d’una vibració no repetitiva, l’espectre no és harmònic i llavors es parla de freqüències parcials.
La superposició de dues vibracions simples de freqüències molt properes però no idèntiques condueix a una vibració complexa que gairebé és periòdica (amb freqüència propera a la de les vibracions simples) i que presenta una fluctuació d’amplitud al llarg del temps. Aquesta fluctuació es coneix amb el nom de batement, i té una freqüència igual a la diferència entre les freqüències de les vibracions simples.
Freqüències de ressonància
L’anàlisi de Fourier té un interès especial quan s’aplica a moviments lliures. En aquest cas, els moviments simples que formen l’espectre s’anomenen modes propis, i corresponen a moviments lliures que el sistema pot realitzar de manera independent. Les freqüències associades als modes propis s’anomenen freqüències pròpies o de ressonància del sistema. Per a poder observar cada mode propi per separat, cal escollir adequadament les condicions inicials de desplaçament i velocitat responsables del moviment del sistema. En el cas d’analitzar una vibració forçada, els parcials de l’espectre corresponent tenen una realitat matemàtica, però no necessàriament física.
El coneixement de les freqüències de ressonància d’un sistema és important per dos motius. En primer lloc, perquè són les integrants de tots els moviments lliures que el sistema pot realitzar. La col·laboració o no d’un mode propi en un moviment lliure arbitrari depèn de la manera com s’ha posat en oscil·lació el sistema. En termes físics, aquesta configuració inicial imposada al sistema des de l’exterior rep el nom de "condicions inicials" i consisteix en el conjunt de desplaçaments i velocitats que es comuniquen al sistema. Així, una corda pinçada és un sistema amb condicions inicials de desplaçament a tots els punts (tret dels extrems), i una corda percudida amb un martell és un sistema amb condició inicial de velocitat localitzada a la zona que ha estat en contacte amb el martell.
En segon lloc, el coneixement de les ressonàncies d’un sistema permet d’actuar-hi de manera forçada amb el màxim rendiment possible. Si l’actuació vibratòria externa té una freqüència que coincideix amb una de les ressonàncies, el sistema no oposa gairebé resistència. Llavors, amb un esforç extern mínim s’obté una amplitud de vibració màxima.
Ones
Superposició d’ones d’igual freqüència i amplitud però de sentit de propagació contrari
© Fototeca.cat/ Studi Ferrer
Les ones mecàniques o acústiques són pertorbacions que es propaguen en un medi material sense que hi hagi un desplaçament net de matèria. Aquestes pertorbacions poden ser molt diverses. Així, en el cas d’una col·lisió de vehicles en cadena en una carretera, la pertorbació és un cop, i s’anomena pertorbació impulsional. En el cas d’una oscil·lació provocada manualment en un extrem d’una corda en tensió, es tracta d’una pertorbació vibratòria que es propaga al llarg de la corda. En tots dos exemples, malgrat haver-hi una comunicació de moviment d’un punt a un altre, el sistema (filera de vehicles o corda) es manté globalment en la mateixa posició, sense que hi hagi ni un avanç ni un retrocés net.
Els dos exemples precedents posen de manifest que ona i vibració no són conceptes equivalents. Pot haver-hi ones no vibratòries (cas de la col·lisió en cadena) i vibratòries (cas de la corda). D’altra banda, una vibració no comporta necessàriament una propagació. Tot i que el concepte d’ona implica en principi un fenomen de propagació, la superposició de moviments ondulatoris pot donar lloc de vegades a moviments resultants no propagatius. Per tal de distingir aquests dos casos qualitativament tan diferents, es parla d’ones propagatives i ones estacionàries.
Magnituds associades a les ones propagatives
Una de les magnituds característiques d’una ona propagativa és la velocitat de propagació. Aquesta velocitat, que informa sobre la rapidesa amb què té lloc la transmissió de la pertorbació d’un punt a un altre, no té res a veure amb la velocitat de les partícules del medi que estan afectades de la pertorbació.
La velocitat de propagació depèn de les característiques del medi, mentre que les velocitats que poden assolir les partícules que el formen depenen de l’actuació externa que ha donat lloc a la pertorbació. Així, un cop fort en una corda de piano provoca una velocitat elevada en el punt de percussió, mentre que un cop feble sobre la mateixa corda li provoca una velocitat baixa. En ambdós casos, però, la velocitat de propagació al llarg de la corda és la mateixa. Quan la direcció de la velocitat de propagació és la mateixa que la de la velocitat de les partícules del medi, es diu que l’ona propagativa és longitudinal. Si aquestes dues direccions són perpendiculars, llavors l’ona propagativa és transversal. L’ona associada a una col·lisió en cadena és longitudinal, mentre que la que es genera en una corda de piano és transversal.
Un altre concepte important associat a les ones propagatives és el de front d’ona. El front d’ona és la superfície formada per tots els punts del medi que reben simultàniament la pertorbació. La geometria d’aquest front canvia segons el tipus de medi i de pertorbació inicial. Així, si es dona un cop amb el palmell de la mà a l’entrada d’un tub cilíndric buit (és a dir, d’una columna d’aire cilíndrica), el front d’ona és aproximadament pla i transversal al tub. Si es punxa un globus molt petit amb una agulla a l’aire lliure (la qual cosa és equivalent a una pertorbació inicial en un sol punt dins d’un medi tridimensional), el front d’ona és molt aproximadament esfèric. Si es deixa caure una pedra dins d’un bassal d’aigua, el front d’ona superficial és inicialment circular.
El pas d’una ona propagativa per un medi modifica no solament l’estat de moviment de les partícules sinó també l’estat de compressió o dilatació intern. En altres termes, l’ona transporta energia cinètica (associada al moviment) i energia potencial (associada a la compressió). L’energia total (o energia mecànica) que travessa una secció, perpendicular a la direcció de propagació, d’un metre quadrat en un segon s’anomena intensitat de l’ona, i la intensitat total associada a tota la superfície d’un front d’ona rep el nom de potència de l’ona.
Si els efectes dissipatius són negligibles, la potència es manté constant, però no passa necessàriament el mateix amb la intensitat. En el cas d’un front d’ona esfèric produït per una pertorbació puntual (o per una font puntual), l’energia mecànica s’ha de repartir sobre una superfície que és més gran com més allunyada es troba de la font, i per tant la intensitat decreix a mesura que augmenta la distància. En el cas d’un front d’ona pla, en canvi, la superfície del front d’ona es manté constant i, per tant, també ho fa la intensitat.
Encara que la intensitat i la potència es mesuren de manera absoluta en watts per metre quadrat i watts, respectivament, és usual donar-ne el nivell respecte d’un valor de referència. La unitat relativa que correspon al quocient entre la magnitud (intensitat o potència) i el valor de referència, expressat en escala logarítmica, és el decibel (dB).
La facilitat amb què una ona es propaga en un medi es resumeix en el concepte d’impedància, que expressa la relació entre la velocitat de les partícules del medi i la força que cal fer per a aconseguir-la. Per a comunicar una mateixa velocitat, un medi dimpedància demana més esforç que un de baixa impedància. L’invers de la impedància és l’admitància (quocient entre la força i la velocitat). Proper a l’admitància, però no sinònim, hi ha el concepte de compliància, que és el quocient entre la força i el desplaçament que produeix. En un medi uniforme infinit, totes aquestes característiques dinàmiques són constants.
Fenòmens relacionats amb la propagació d’ones
Hi ha diversos fenòmens associats a la propagació d’ones: reflexió, transmissió, refracció, absorció i difracció. Així com la reflexió es relaciona únicament amb un canvi brusc de medi de propagació, els altres (tret de la difracció) es poden produir també quan el medi canvia de propietats de manera gradual (a causa, per exemple, d’un canvi de temperatura). La difracció, en canvi, prové de la interacció d’un front d’ona amb un objecte petit immers en el medi o bé del pas d’un front a través d’un orifici. Tant els canvis bruscos de medi de propagació com els graduals dins d’un mateix medi impliquen canvis (bruscos o graduals) d’impedància (o de qualsevol de les altres magnituds que s’associen a les característiques dinàmiques del medi).
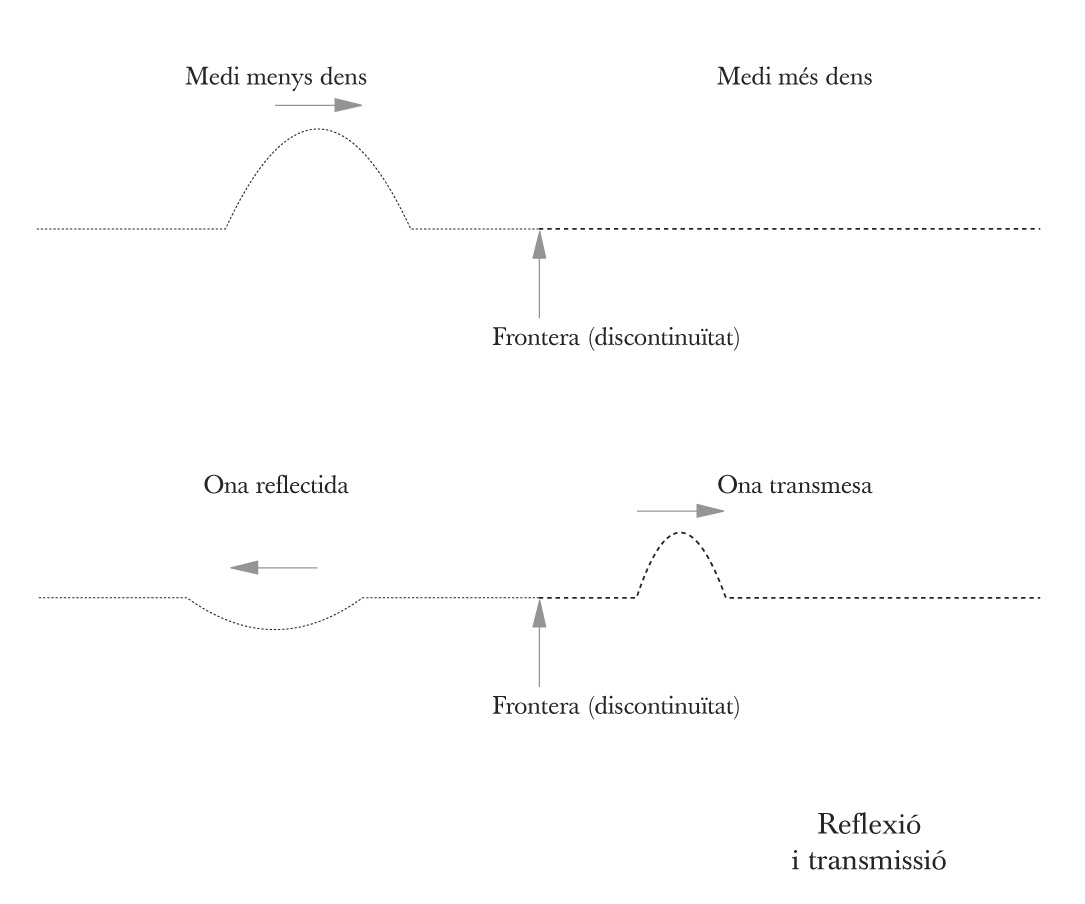
Reflexió i transmissió
La reflexió és el fenomen pel qual una ona que es propaga en un medi retorna parcialment en incidir sobre un segon medi de característiques dinàmiques diferents. Si la reflexió no és total, part de l’ona passa a propagar-se en el segon medi. Aquest fenomen s’anomena transmissió. Quan l’ona original incideix sobre un medi d’impedància molt més alta (o admitància molt més baixa) que la del medi inicial, la reflexió és molt important i la transmissió és molt baixa. En cas contrari, la reflexió és baixa i la transmissió, alta.
En el context de l’acústica de recintes (acústica de sales), la reflexió de les ones sonores a les parets és directament responsable del temps de reverberació i de la repartició del so dins la sala (pot redirigir-lo cap a les zones on no arriba de manera directa).
En el context de l’acústica dels instruments musicals, l’equilibri entre la intensitat i la durada dels sons que es perceben depèn directament de processos de reflexió-transmissió. En els instruments autoexcitats, a més, és essencial per a controlar el mecanisme d’autoexcitació primari i garantir l’estabilitat dels sons.
En un procés de reflexió-transmissió, l’energia mecànica que transporta l’ona inicial s’ha de repartir entre les dues ones resultants. Per aquest motiu, l’ona reflectida i l’ona transmesa tenen una intensitat inferior a la incident.
Refracció
En la refracció, l’ona reflectida té una direcció o un sentit de propagació diferents de l’ona inicial, mentre que l’ona transmesa només canvia de direcció de propagació (respecte de la inicial) quan la velocitat de propagació en el segon medi és diferent. Aquest canvi en la velocitat i direcció de propagació associat al canvi de medi es coneix amb el nom de refracció, i llavors l’ona transmesa es pot anomenar ona refractada. La refracció pot tenir lloc també quan el medi canvia gradualment de característiques dinàmiques. En aquest cas, l’ona es refracta sense que hi hagi cap procés de reflexió associat.
Absorció
Els canvis d’intensitat d’una ona propagativa no tan sols es produeixen en els processos de reflexió-transmissió, també poden estar associats a fenòmens d’absorció dins un mateix medi. En aquest cas, la disminució d’intensitat no prové d’una transmissió dmecànica, sinó d’una conversió d’energia mecànica en calor causada per friccions internes al medi. L’absorció és molt important en materials tous i porosos, i és la base dels aïllaments acústics.
Difracció
El fenomen de difracció es produeix per la capacitat que té una ona de rodejar un objecte en funció de la seva mida. Si un front d’ona incideix sobre un objecte petit immers en el medi, aquest es comporta com si fos una nova font puntual que emet ones propagatives en totes les direccions. L’objecte, per tant, no ha estat causa d’una zona d’ombra (no afectada per l’ona), sinó que ha estat envoltat per l’ona. Això comporta un canvi en la geometria del front inicial; si el medi de propagació és tridimensional i el front inicial era pla, el nou front d’ona resulta esfèric. La difracció també es pot produir per incidència d’un front d’ona sobre una frontera rígida que presenta un orifici petit. L’orifici actua com a nova font emissora, i per aquest motiu es veuen aparèixer fronts d’ona esfèrics.
Ones monocromàtiques
Un tipus d’ona propagativa particular és l’anomenada monocromàtica. La propagació d’una ona monocromàtica provoca un moviment vibratori simple de les partícules del medi. En aquest cas, se li poden associar una freqüència (o període) i una amplitud. Si no hi ha dissipacions, l’amplitud és sempre la mateixa per a tots els punts del medi afectats per l’ona si es tracta d’una ona plana, mentre que resulta decreixent en funció de la distància a la font que l’ha originada si es tracta de qualsevol altra geometria (ona esfèrica, cilíndrica...).
L’estat de vibració dels punts del medi afectats per l’ona no és el mateix simultàniament: mentre que en un instant donat alguns poden estar en situació de desplaçament màxim, d’altres poden estar passant per la posició mitjana (o d’equilibri), i d’altres, per posicions intermèdies. Quan dos punts es troben simultàniament en el mateix estat de vibració, es diu que estan en fase; quan es troben en estats oposats (per exemple, tots dos amb desplaçament màxim però a les dues bandes oposades de la posició d’equilibri), es diu que estan en contrafase o oposició de fase. La distància mínima que separa dos punts del medi que estan en fase s’anomena longitud d’ona. En conseqüència, la distància mínima entre dos punts en contrafase correspon a mitja longitud d’ona.
Superposició d’ones monocromàtiques
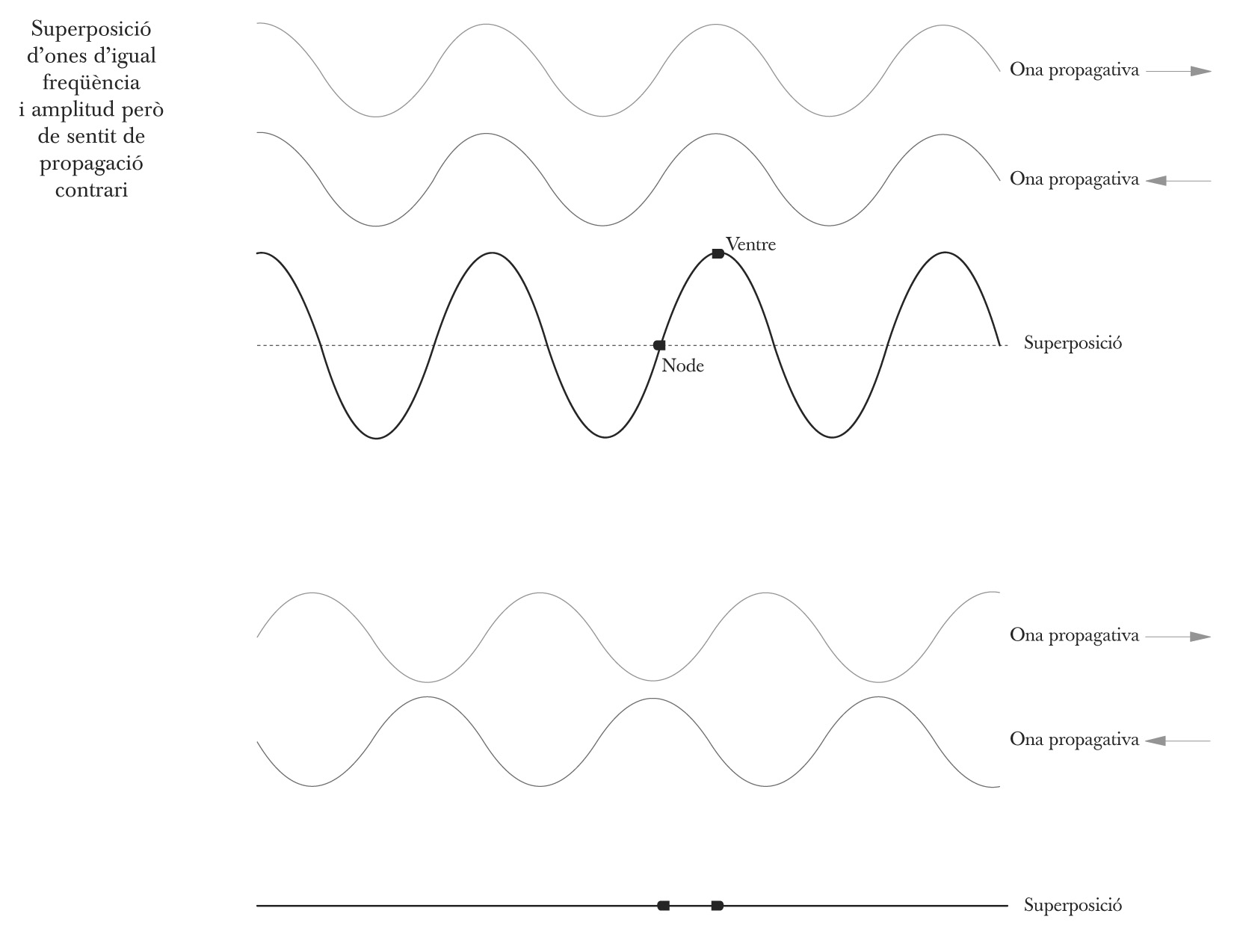
La superposició d’ones propagatives monocromàtiques pot donar lloc a ones complexes resultants de caràcter molt divers. L’anàlisi de Fourier es pot aplicar també a aquest problema. Així, només si les freqüències de les ones monocromàtiques formen un conjunt harmònic (és a dir, són múltiples enters d’una mateixa freqüència fonamental), l’ona resultant és periòdica. El problema invers també es pot tractar amb l’anàlisi de Fourier: tota ona propagativa es pot descompondre en un conjunt d’ones monocromàtiques, les freqüències de les quals formen l’espectre de l’ona inicial. Un cas particularment interessant és el de la superposició de dues ones de la mateixa freqüència i amplitud que es propaguen en la mateixa direcció però en sentits oposats. El resultat n’és una vibració en la qual ha desaparegut tot indici de propagació i que s’anomena ona estacionària. En efecte, hi ha punts del medi que oscil·len entre valors d’amplitud màxima i que s’anomenen ventres; d’altres es troben permanentment en repòs, i s’anomenen nodes; i d’altres oscil·len amb amplituds intermèdies. Dos ventres o dos nodes consecutius estan separats mitja longitud d’ona. A cada instant de temps, tots els punts del medi (tret dels nodes) estan en fase o en contrafase; dit d’una altra manera, tots assoleixen simultàniament la posició de màxim desplaçament a una banda o l’altra de la posició d’equilibri.
L’aparició d’una ona estacionària pot ser el resultat d’un procés de reflexió. Si una ona monocromàtica inverteix el seu sentit de propagació a causa d’una reflexió total (és a dir, sense que hi hagi transmissió i, per tant, de manera que l’ona reflectida té la mateixa amplitud que l’ona inicial), la superposició de l’ona incident i la reflectida condueix a una ona estacionària.
El diferent comportament dels medis mecànics o acústics davant les freqüències a què són sotmesos (màxima resposta quan aquestes coincideixen amb alguna de les seves ressonàncies) i el fet que tota ona es pot descompondre en un conjunt d’ones monocromàtiques fan que la forma d’una ona complexa es modifiqui en general quan canvia de medi de propagació. En efecte, la facilitat o dificultat amb què una ona es propaga en un medi (en altres paraules, la impedància o l’admitància del medi) no és constant, sinó que depèn de la freqüència. Així, la impedància és baixa (o l’admitància és elevada) per a les freqüències de l’ona que coincideixen amb les ressonàncies del medi, mentre que succeeix el contrari per a les que estan lluny de les ressonàncies. Això fa que algunes de les freqüències de l’espectre de l’ona original siguin amplificades, mentre que les altres són atenuades. Tots aquests canvis en l’espectre impliquen necessàriament la deformació de l’ona.
Bibliografia
- Crawford, F.S.: Waves. Berkeley Physics Course, vol. 3, McGraw-Hill Book Company, Londres 1968
- Fletcher, N.H. i Rossing, Th.D.: The Physics of Musical Instruments, Springer-Verlag, Nova York 1990
- Rossing, Th.D.: The Science of Sound, Addison-Wesley Publishing Company, Nova York 1990
- Wood, A.: The Physics of Music, University Paperbacks, Methuen Co Ltd, Londres 1969