Resultats de la cerca
Es mostren 5 resultats
curvatura de l’espai
Astronomia
Física
En el marc de la relativitat general, propietat geomètrica de l’espaitemps per la qual aquest es corba a causa de la presència de matèria.
El moviment de les masses és entès com un moviment lliure al llarg de les geodèsiques de l’espaitemps, en lloc d’ésser-ho en termes de la interacció gravitacional El tensor de curvatura explicita matemàticament aquesta propietat
braquistòcrona
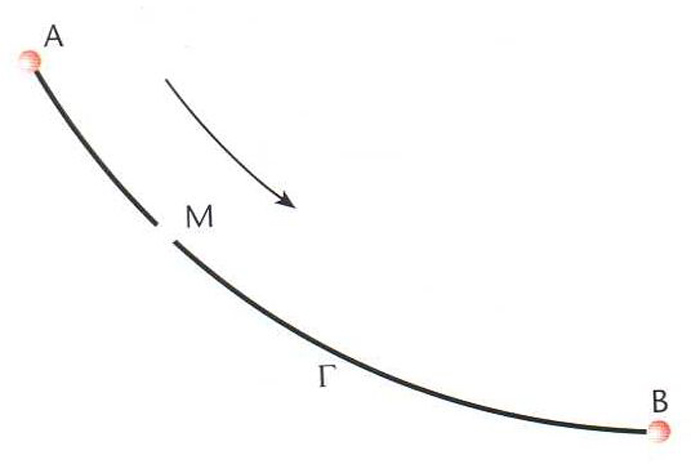
Braquistròcrona
© fototeca.cat
Física
Corba que ha de recórrer una partícula que parteix del repòs i es mou per l’acció del pes i sense fregament, per tal d’unir dos punts fixs A
i B
en el mínim de temps possible.
La solució de l’eqüació diferencial que explicita analíticament el problema és una cicloide El problema de trobar aquesta corba és famós en la història de la matemàtica, car conduí Johann Bernoulli a l’establiment formal del càlcul de variacions variació
experiment
Física
Tecnologia
Producció artificial i controlada d’un fenomen per tal de dur a terme la comprovació d’una hipòtesi.
El concepte d’experiment inclou el conjunt d’operacions de tipus heurístic encaminades a donar solidesa a la formulació d’una hipòtesi basada en una sèrie de suposicions més o menys vagues Per tant, un experiment només és possible si hi resten especificades de forma explícita les condicions de comprovació d’una hipòtesi, si aquestes condicions es poden produir voluntàriament i si hom pot controlar determinats factors En general, la informació obtinguda per mitjà de l’experimentació és representada quantitativament i són els mètodes estadístics els que permeten de determinar la relació…
termoestàtica
Física
Branca de la termodinàmica que estudia els sistemes tèrmics en equilibri tot basant-se en dades macroscòpiques i que requereix que els processos estudiats no depenguin, com a variable explícita, del temps.
Els mètodes termoestàtics indiquen el sentit d’un procés de canvi, però no la velocitat del canvi
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un espai vectorial de dimensió…