Resultats de la cerca
Es mostren 11 resultats
principi de Hamilton
Física
Una de les formes d’enunciar el principi de la mínima acció.
L' acció elemental és definida a partir del lagrangià, dA = L dt , i el principi afirma que el moviment del sistema entre dos instants t 1 i t 2 és tal que l’acció és un extremal, és a dir, un màxim o un mínim Hom en dedueix les equacions de Lagrange
equacions de Hamilton
Física
Equacions del moviment d’un sistema dinàmic de hamiltonià H, donades per
i per:
on t és el temps, les qi són les coordenades generalitzades i les pi els corresponents moments canònics del sistema.
equació de Hamilton-Jacobi
Física
En l’estudi del moviment d’un sistema físic, equació expressada per la fórmula H essent el hamiltonià del sistema, les qi, les coordenades generalitzades, t el temps, i S la incògnita, anomenada funció principal de Hamilton.
La resolució de l’equació permet de determinar les equacions del moviment del sistema
Bertram N. Brockhouse
Física
Físic canadenc.
Estudià a la Universitat de Toronto S'especialitzà en el comportament dels materials a temperatures extremes i especialment en la difracció de neutrons com a mitjà de determinació estructural Per aquestes investigacions rebé el premi Nobel de física el 1994, juntament amb CGShull
principi variacional
Física
Proposició segons la qual un sistema físic macroscòpic aïllat de l’exterior evoluciona de manera que fa extremal la integral de la funció que el representa dinàmicament, calculada entre l’estat inicial i el final.
Quan el principi variacional és aplicat a la funció de Lagrange de la mecànica hom l’anomena principi de la mínima acció, o de Hamilton , i si és aplicat a la trajectòria d’una ona electromagnètica en resulta el principi de Fermat , mentre que si ho és a un procés de reacció exotèrmic és anomenat principi de Thomsen-Berthelot
dinàmica
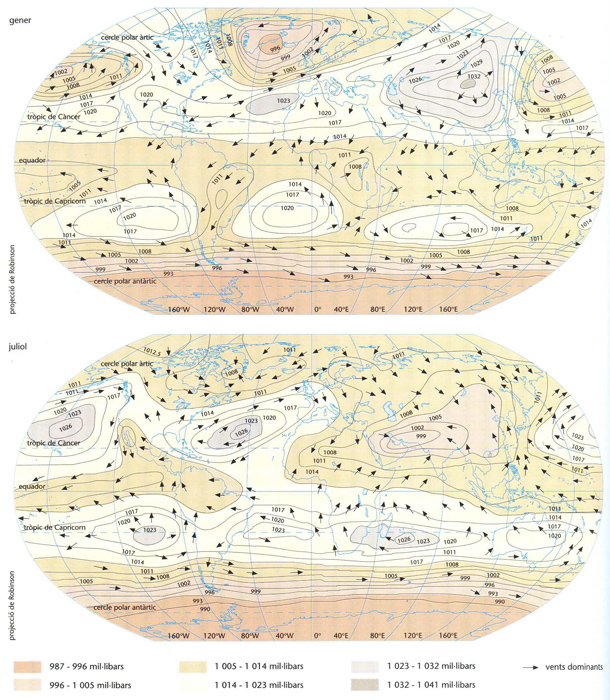
Mapa de les pressions mitjanes al nivell de la mar pel gener i el juliol (en mil·libars) amb la direcció dels vents dominants
© Fototeca.cat
Física
Branca de la mecànica
que estudia els moviments dels cossos en tant que són produïts per l’aplicació de les forces.
Malgrat que sovint hom diferenciï entre dinàmica i estàtica, la separació entre aquestes dues branques de la mecànica no és estricta, puix que, si hom té en compte la hipòtesi de D’Alembert sobre les forces d’inèrcia, la dinàmica pot ésser considerada, des d’un punt de vista formal, com un apartat de l’estàtica En física clàssica, les lleis de la dinàmica tenen un caràcter determinista donades unes condicions inicials que fixen la posició i la velocitat d’un mòbil en un instant determinat, la teoria permet, en principi, la predicció del moviment en el futur i el coneixement de la seva…
teoria clàssica de camps

Esquema de la teoria clàssica de camps
© Fototeca
Física
Part de la física que estudia els sistemes que són descrits per camps i l’evolució dels quals és predicible (és a dir, que l’estat en un instant t determina totalment l’estat a tot instant posterior t’).
Conceptualment, la teoria pot ésser estructural si les magnituds són les dels components microscòpics, com ara és el cas de l' electrodinàmica clàssica i la relativitat general , o fenomenològica si les magnituds macroscòpiques tenen una interpretació indirecta en termes de la configuració microscòpica, com ara és el cas de la mecànica dels medis continus La dinàmica dels camps clàssics pot ésser derivada d’un principi integral anàleg al principi de Hamilton de la mecànica clàssica, i en resulten les equacions de Lagrange del camp i els teoremes de conservació que són…
Donna Strickland

Donna Strickland
© Abdullah Rahnama
Física
Física canadenca.
Es graduà per la Universitat McMaster de Hamilton Ontario el 1981 Posteriorment començà, sota la direcció de Gérard Mourou , la tesi doctoral a la Universitat de Rochester Nova York En aquests treballs dissenyà, amb Mourou, una tècnica per a l’obtenció d’impulsos làser de màxima intensitat i durada ultracurta, coneguda per la sigla CPA de l’anglès chirped pulse amplification , que ha donat lloc a importants aplicacions en física nuclear, física de partícules i cirurgia ocular Per aquesta aportació, rebé el premi Nobel de física el 2018 la tercera dona guardonada amb aquest premi…
principi de Maupertuis
Física
Forma simplificada del principi de Hamilton de la mecànica analítica que permet de trobar la trajectòria d’una partícula sense cap referència al temps, posat que la funció de Hamilton de la partícula no depengui explícitament del temps.
Enunciat primitivament per Maupertuis, de qui pren el nom, fou establert en forma matemàtica per Euler i Lagrange finalment, Jacobi el posà en la forma , on m és la massa de la partícula, E l’energia total, U l’energia potencial, quan la partícula és sotmesa a forces conservadores, i dl un element de longitud de la trajectòria