Resultats de la cerca
Es mostren 30 resultats
refracció
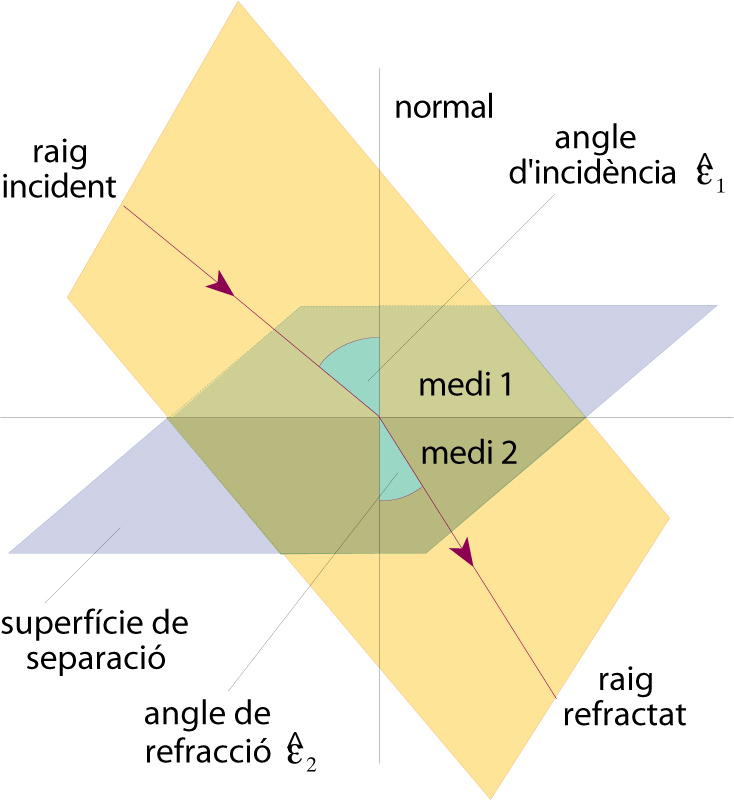
Trajectòria dels raigs en la refracció quan el medi 2 és més dens que el medi 1
© Fototeca.cat
Física
Modificació de la trajectòria d’un raig o del front d’una ona quan travessa una superfície que limita dos medis diferents.
En el cas particular dels raigs, hom pot provar que el raig incident, la normal a la superfície en el punt d’incidència i el raig refractat són coplanaris, i que la relació entre l' angle d’incidència ê 1 , i el de refracció ê 2 és donada per la llei de Snellius n 1 sin ê 1 = n 2 sin ê 2 , on n 1 i n 2 són els índexs de refracció de cadascun dels medis materials separats per la superfície considerada Quan té lloc la refracció d’una ona en una superfície, simultàniament hi ha una reflexió parcial, per la qual cosa resta disminuïda la intensitat de l’ona refractada respecte a la de…
angle límit
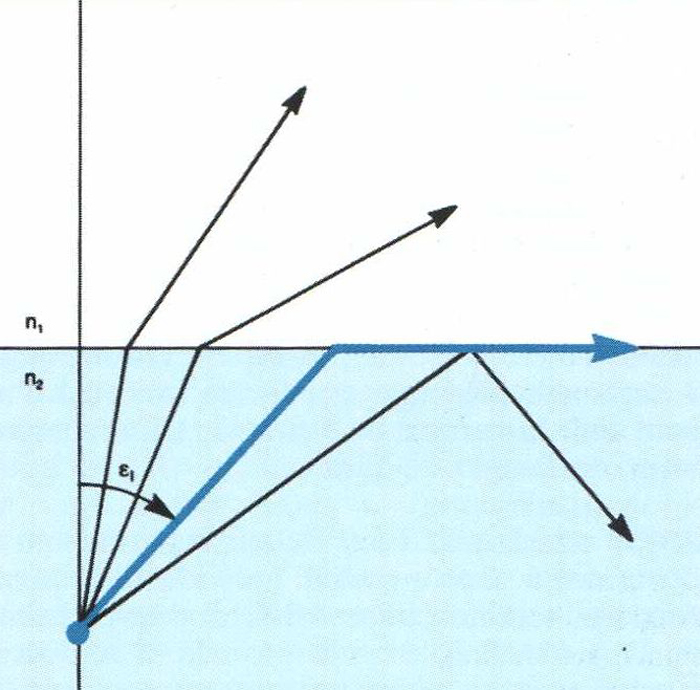
Angle límit Esub1 entre dos medis d’índex de refracció n i n' ( n>n' ; per a angles d’incidència E > Esubl hi ha una refracció total
© fototeca.cat
Física
En passar la llum d’un medi d’índex de refracció n
a un altre d’índex menor n´
(cas, p ex, de l’aigua a l’aire), valor mínim de l’angle d’incidència a partir del qual té lloc la reflexió total
.
D’acord amb la llei de la refracció resulta que sin ε 1 = n'/n Un raig que incideixi amb un angle menor és refractat, mentre que si no ho fa amb un angle més gran és reflectit, i actua així la interfície com a un mirall
sistema òptic
Física
Col·lecció de superfícies que separen medis transparents a la llum.
Tenen interès els sistemes plans superfícies planes i els sistemes centrals superfícies de revolució entorn d’un eix comú Un sistema òptic es caracteritza pels seus elements cardinals , que són els seus punts i plans focals, principals i nodals elements cardinals d’un sistema òptic
dioptre
Física
Superfície que separa dos medis transparents de diferent índex de refracció.
Segons que la superfície sigui plana o esfèrica, hom parla de dioptres plans o de dioptres esfèrics
Pieter Zeeman
Física
Físic neerlandès.
Féu importants recerques sobre òptica, radiacions, propagació de la llum en diversos medis, teoria dels colors, etc El 1896 descobrí amb HLorentz l’efecte que duu el seu nom, per la qual cosa compartí amb Lorentz el premi Nobel de física el 1902 Les seves investigacions han confirmat plenament la teoria de la relativitat
transmissivitat
Física
Relació entre l’energia transmesa i la incident en un feix d’ones electromagnètiques.
En el cas d’un feix refractat, la transmissivitat T és expressada on I és la intensitat dels feixos el subíndex 1 es refereix al medi d’incidència i el 2 al de refracció, n 1 i n 2 són els índexs de refracció dels medis 1 i 2, i φ l’angle que formen amb la normal També és anomenat poder de transmissió
reflexió total
Física
Fenomen pel qual quan una ona passa d’un medi més refringent a un altre de menys refringent (refracció).
Hi ha un angle d’incidència màxim î tal que tots els raigs que incideixen amb un angle més gran que aquest no passen al segon medi ni tan sols parcialment, sinó que són reflectits un altre cop cap al medi d’on procedeixen Hom pot demostrar que l’angle l , anomenat angle límit , només depèn dels índexs de refracció n 1 i n 2 dels dos medis aquest angle és donat per la fórmula sin l = n 2 / n 1 essent n 2 < n 1
refractiu | refractiva
Física
Dit de la superfície de separació de dos medis de diferent índex de refracció.
Ernst Chladni
Física
Físic alemany.
Inventà dos instruments músics, l’eufoni i el clavicilindre, variants de l’harmònica de cristall, i a través de la música començà a estudiar el so i esdevingué un dels fundadors de l’acústica Descobrí vibracions longitudinals en cordes o barres i estudià experimentalment la vibració de plaques en les quals, si hom hi escampa sorra fina pel damunt, apareixen les anomenades figures acústiques de Chladni , formades per la sorra acumulada en les línies nodals de la placa en vibració Explicà el fenomen de ressonància en els diapasons i efectuà mesures sobre la velocitat del so en medis…
equacions de Maxwell
Física
Equacions fonamentals de l’electromagnetisme, formulades per J.C.Maxwell entre el 1862 i el 1873.
Per a medis materials en repòs, hom les pot enunciar matemàticament així div E = ρ/ε 0 1 div B = 0 2 rot E = ∂ B /∂ t 3 rot B = μ 0 j +ε 0 ∂ E /∂ t 4 El mèrit principal de Maxwell consistí a reunir sota un mateix formalisme els coneixements que hom ja tenia dels fenòmens electromagnètics gràcies als estudis anteriors d’Ampère, Faraday, etc —equacions 1, 2 i 4—, alhora que proposà l’equació 3 per representar els efectes elèctrics d’un camp magnètic variable en el temps Una conseqüència immediata d’aquestes equacions és la possibilitat teòrica de la propagació d’ones…