Resultats de la cerca
Es mostren 6 resultats
con de llum
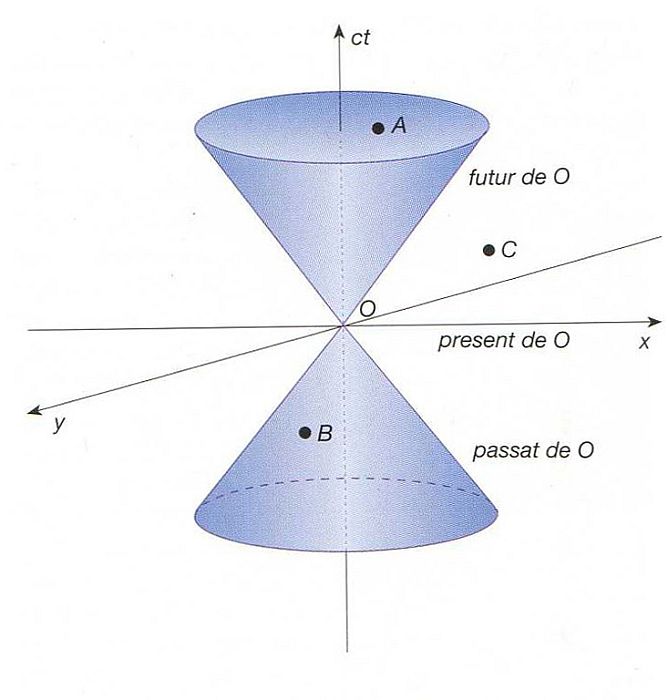
Representació en dues dimensions espacials del con de llum tetradimensional de l’esdevenimentO
©
Física
A l’espaitemps tetradimensional de la relativitat especial, figura que palesa gràficament el significat dels conceptes passat, present i futur d’un esdeveniment qualsevol O.
És una superfície hipercònica de dos fulls formada pels esdeveniments separats de l’esdeveniment O origen de coordenades per un 4-interval tipus-llum Δ s 2 = c 2 Δ t 2 - |Δ r | 2 = 0 Els punts A de l’interior del con de llum que satisfan Δ s 2 > 0 amb Δ t > 0, formen el con del futur o simplement, el futur de l’esdeveniment 0 els punts B de l’interior del con de llum que satisfan Δ s 2 > 0 amb Δ t < 0, formen el con del passat O , simplement, el passat de O els punts C de l’exterior del con de llum, que satisfan Δ s 2 < 0, formen el…
llei de Beer
Física
Llei que permet de calcular la disminució de la intensitat d’un raig de llum, o d’una radiació electromagnètica semblant, després d’haver travessat una solució.
La quantitat de llum absorbida I és donada per l’expressió essent la intensitat del raig de llum incident, b el coeficient d’absorció per unitat de concentració de solut, que depèn de la longitud d’ona de llum emprada, c la concentració de la solució, i x el gruix travessat per la radiació L' absorbància de les substàncies que satisfan la llei de Beer és proporcional a la concentració
quantitat de moviment
Física
Per a un punt material de massa m, vector p definit per p=m v, on v és la velocitat del punt material.
És anomenat també moment lineal del punt La seva variació en el temps, d p/ dt , és relacionada amb la resultant R de les forces que actuen sobre el punt mitjançant l’expressió d p/ dt= R Per a un sistema de punts, hom defineix la quantitat de moviment del sistema per Si v G és la velocitat del centre de masses del sistema, aleshores se satisfà que P = M v G , on és la massa total del sistema Si les forces internes que s’exerceixen mútuament els punts del sistema satisfan la llei d’acció i reacció tercera llei de Newton, aleshores la variació temporal de P és igual a la…
llei de conservació
Física
Llei que expressa que el valor d’una magnitud física d’un sistema físic roman constant en el temps durant determinades transformacions.
Cal distingir entre les lleis de conservació associades a simetries dinàmiques i les lleis de conservació que resulten de simetries més profundes de la natura D’una banda, l’existència d’una llei de conservació d’una variable dinàmica com és ara l’energia, permet que, en analitzar l’evolució del sistema, hom pugui rebutjar totes aquelles solucions que, si bé són possibles per tal com satisfan l’equació dinàmica, no s’adiuen amb la conservació admesa per tant, el coneixement de les lleis de conservació simplifica notablement el tractament dels problemes, alguns dels quals serien, altrament,…
estat
Física
Electrònica i informàtica
Manera d’ésser, existir o presentar-se un sistema material.
L’estat d’un sistema es defineix per un nombre determinat de magnituds físiques expressables quantitativament, anomenades variables o funcions d’estat els valors de les quals en un instant t o permeten de caracteritzar la dinàmica d’un sistema, i contenen prou informació sobre la seva història anterior a t o perquè hom pugui determinar-ne el comportament partint del coneixement del seu estat en t o i de les entrades posteriors a t o Dins un sistema poden existir diversos conjunts de variables d’estat, tots ells interrelacionats un dels més comuns és el de les variables de fase , format per…
teorema de Bloch
Física
Teorema segons el qual les solucions de l’equació de Schrödinger per a un electró que es mou en el si d’un potencial periòdic (p ex, el potencial en un cristall) és periòdic respecte a translacions T sobre la malla: U (r + T = U (r)) satisfan l’expressió.
ψ r + T = e i k T ψ r , essent k el vector d’ona aquestes funcions s’anomenen funcions de Bloch Una expressió equivalent a l’anterior és ψ k, r = e i k r u k, r , essent u una funció amb la mateixa periodicitat que el potencial u k, r + T = u k, r La funció d’ona ψ és, doncs, una ona plana modulada a cada cella per la funció periòdica u k, r Aquest teorema rep a vegades el nom de teorema de Floquet