Resultats de la cerca
Es mostren 20 resultats
Sin-itiro Tomonaga
Física
Físic japonès.
Estudià a Tòquio, a Kyoto i a Leipzig Elaborà una teoria sobre l’electrodinàmica quàntica i féu recerques importants en física atòmica, dinàmica quàntica i electromagnetisme El 1965 li fou atorgat el premi Nobel de física, juntament amb RPFeynman i JSSchwinger
amplitud
Física
Valor màxim que pren una magnitud vibratòria o oscil·lant en un semiperíode.
Quan la magnitud vibratòria pot ésser expressada per una funció sinusoidal del tipus ft = A sin οt + ϕ, l’amplitud val A i correspon al cas en què sin οt + ϕ val 1
fórmula de Clairaut
Física
Fórmula que dóna el valor de l’acceleració de la gravetat g en un punt de latitud φ.
L’expressió teòrica és g = g e 1 + 5ω 2 a /2 g e - e sin 2 φ, on g e és el valor de la gravetat a l’equador, a és el semieix major equatorial de l’ellipsoide de referència, e és la seva ellipticitat i w és la velocitat angular de la Terra El valor numèric és donat per l’expressió g = 978,049 1-0,0052884 sin 2 φ, on hom ha pres com a ellipsoide de referència un d’aplatament 1/297
angle límit
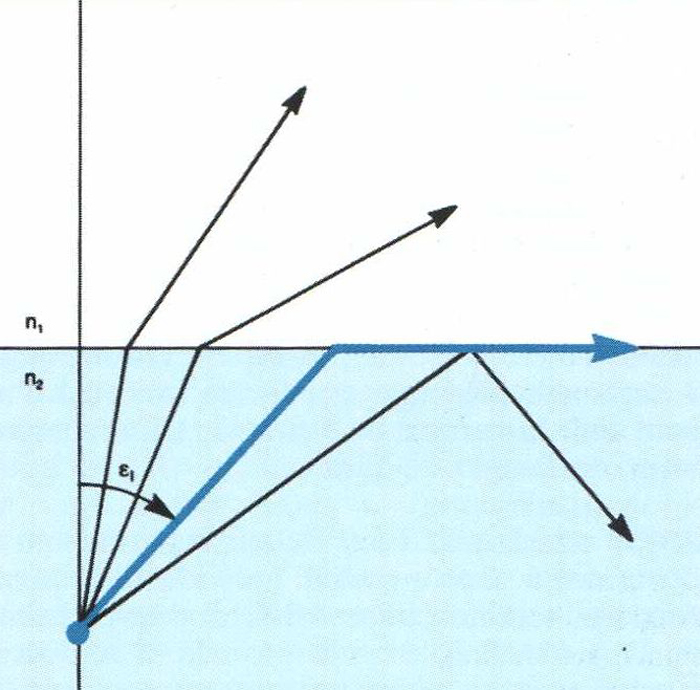
Angle límit Esub1 entre dos medis d’índex de refracció n i n' ( n>n' ; per a angles d’incidència E > Esubl hi ha una refracció total
© fototeca.cat
Física
En passar la llum d’un medi d’índex de refracció n
a un altre d’índex menor n´
(cas, p ex, de l’aigua a l’aire), valor mínim de l’angle d’incidència a partir del qual té lloc la reflexió total
.
D’acord amb la llei de la refracció resulta que sin ε 1 = n'/n Un raig que incideixi amb un angle menor és refractat, mentre que si no ho fa amb un angle més gran és reflectit, i actua així la interfície com a un mirall
refracció
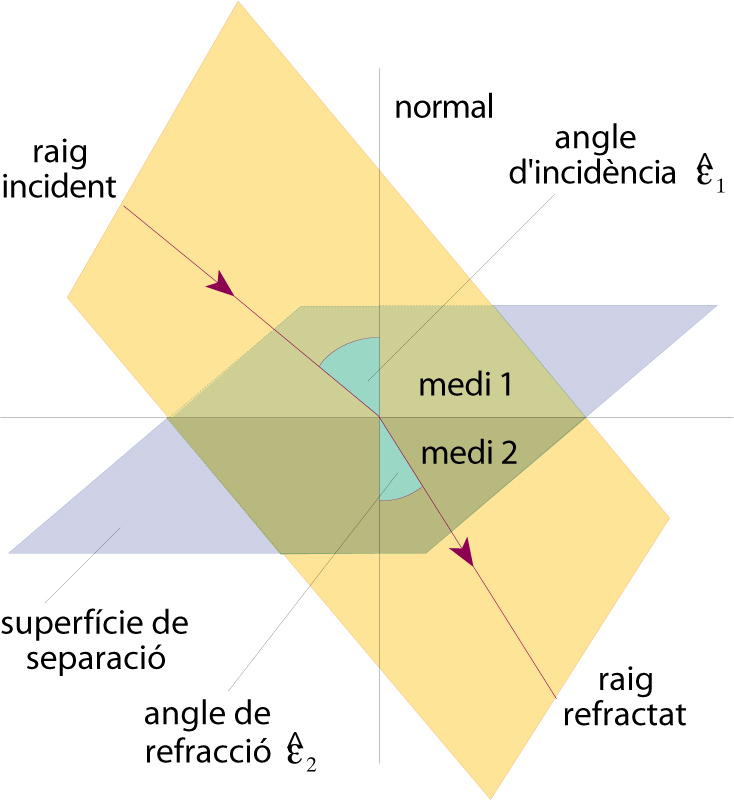
Trajectòria dels raigs en la refracció quan el medi 2 és més dens que el medi 1
© Fototeca.cat
Física
Modificació de la trajectòria d’un raig o del front d’una ona quan travessa una superfície que limita dos medis diferents.
En el cas particular dels raigs, hom pot provar que el raig incident, la normal a la superfície en el punt d’incidència i el raig refractat són coplanaris, i que la relació entre l' angle d’incidència ê 1 , i el de refracció ê 2 és donada per la llei de Snellius n 1 sin ê 1 = n 2 sin ê 2 , on n 1 i n 2 són els índexs de refracció de cadascun dels medis materials separats per la superfície considerada Quan té lloc la refracció d’una ona en una superfície, simultàniament hi ha una reflexió parcial, per la qual cosa resta disminuïda la intensitat de l’ona refractada…
pla inclinat
Física
Pla que forma un cert angle amb el pla horitzontal.
És considerat com una de les màquines simples i permet d’elevar un cos de pes P amb una força F molt més petita que P Si hom desestima el fregament entre el cos i el pla inclinat, la força F necessària per a elevar el cos és donada per la fórmula F = P sin a
vorticitat
Meteorologia
Física
Magnitud que mesura el moviment de rotació de les partícules d’un fluid.
És utilitzada en la dinàmica de fluids Es considera que un fluid té vorticitat positiva quan el moviment és ciclònic sentit antihorari a l’hemisferi nord i el contrari a l’hemisferi sud i vorticitat negativa quan és moviment anticiclònic moviment horari a l’hemisferi nord i el contrari al sud En fluids geofísics com és l’oceà, la vorticitat planetària es defineix per f=2Ω sin α, on α és la latitud
reflexió total
Física
Fenomen pel qual quan una ona passa d’un medi més refringent a un altre de menys refringent (refracció).
Hi ha un angle d’incidència màxim î tal que tots els raigs que incideixen amb un angle més gran que aquest no passen al segon medi ni tan sols parcialment, sinó que són reflectits un altre cop cap al medi d’on procedeixen Hom pot demostrar que l’angle l , anomenat angle límit , només depèn dels índexs de refracció n 1 i n 2 dels dos medis aquest angle és donat per la fórmula sin l = n 2 / n 1 essent n 2 < n 1
xarxa de difracció
Física
Superfície transparent (plana) o reflectora (plana o còncava) on són gravades un seguit d’estries (o traços), rectilínies, idèntiques, paral·leles i equidistants i que hom empra generalment com a sistema dispersor de radiació policromàtica.
Si la superfície és plana hom parla de xarxa plana i, si és còncava, de xarxa còncava Les estries poden ésser gravades sobre una superfície transparent plana xarxa transmissora , o sobre una superfície metàllica, plana o còncava xarxa reflectora , o bé poden ésser les franges d’una imatge hologràfica impressionada sobre un material sensible xarxa hologràfica Hom empra també la xarxa esglaonada , en què les estries formen un perfil de dent de serra En el cas d’una xarxa transmissora, si una ona plana incideix sobre la seva superfície amb un angle d’incidència i , hom pot considerar que la…
poder dispersiu
Física
Característica d’un medi transparent a la radiació electromagnètica.
Es defineix com la relació entre la diferència de les desviacions D de les ratlles F i C de l’hidrogen, de longituds d’ona λ F = 0,486 μm i λ C = 0,656 μm, i la desviació de la ratlla D del sodi, de longitud d’ona λ D = 0,589 μm, en travessar un prisma d’angle ϕ petit és a dir ϕ ≈ sin ϕ, fet amb el material que constitueix aquest medi El poder dispersiu K és expressat per on n F , n C i n D són els índexs de refracció del medi per a les longituds d’ona corresponents a les diferents ratlles L’invers del poder dispersiu és anomenat constringència