Resultats de la cerca
Es mostren 3 resultats
vapor saturat
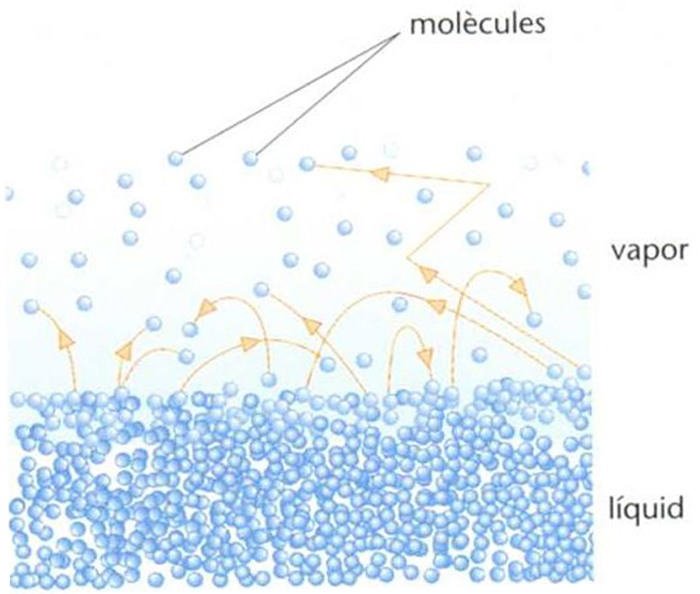
Representació del vapor saturat : en un instant donat, hi ha tantes molècules que es vaporitzen com molècules que es condensen
© Fototeca.cat
Física
En un recinte tancat o que es pugui considerar com a tal, dit del vapor d’una substància que és en equilibri amb la fase líquida d’aquesta, és a dir, que en un instant donat, per a unes determinades condicions de pressió i de temperatura, el nombre de molècules que es condensen i de molècules que es vaporitzen és el mateix.
Hom pot condensar totalment el vapor saturat d’un recinte tancat mitjançant l’inici d’una operació de compressió o de refredament, sense que la pressió ni la temperatura variïn mentre hi resti vapor per condensar
balança automàtica
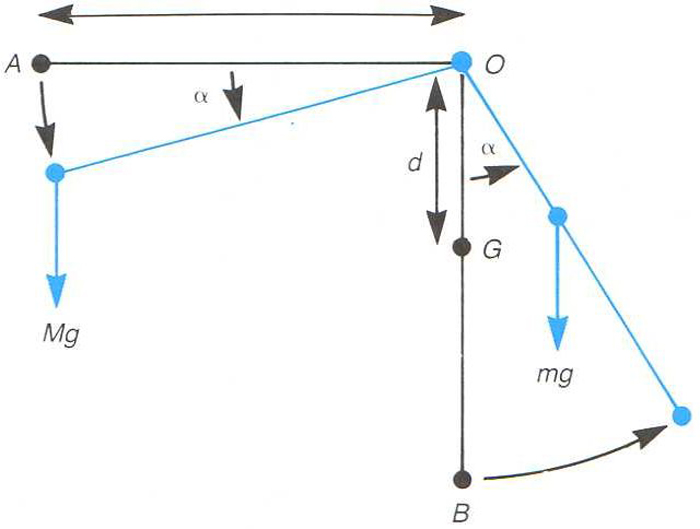
Esquema de funcionament d’una balança automàtica
© Fototeca.cat
Física
Balança d’un sol plat que dóna directament la massa mesurada, havent-ne equilibrat ella mateixa la càrrega.
És la balança típica de les transaccions del comerç i la indústria Inicialment de base mecànica, avui les balances electròniques calculen el pes, el preu de la mercaderia un cop fixat el preu de la unitat, i sovint donen una nota impresa que conté els detalls de la pesada L’esquema simplificat d’una balança automàtica consisteix en una palanca colzada AOB , amb fulcre en O , massa m i centre de gravetat G En situar a A una càrrega de massa M , el conjunt girarà un angle α, i en l’equilibri la igualtat de moments respecte a O permetrà d’escriure Mgl cos α = mg d sin α, essent g l’acceleració…
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un espai vectorial de dimensió…