Resultats de la cerca
Es mostren 3270 resultats
teorema de Bolzano-Weierstrass
Matemàtiques
Teorema segons el qual tot conjunt infinit i afitat d’un espai euclidià té almenys un punt d’acumulació i tota successió infinita afitada té almenys un punt límit
teorema de Bolzano-Weierstrass
Matemàtiques
Teorema emprat en l’estudi de màxims i mínims; afirma que per a una funció y(x) contínua a l’interval tancat [a, b] de la recta, hi ha un valor que és màxim absolut i un altre que és mínim absolut.
teorema de Bolzano-Cauchy
Matemàtiques
Teorema referit a l’estudi de la convergència de funcions.
Estableix que la condició necessària i suficient perquè la funció y x sigui convergent en x →η és que, per a cada nombre ε > 0, es compleixi per a tot parell de valors x’, x' d’un cert entorn reduït de η l’acotació | y x' - y x' | < ε Aquest teorema referit a la convergència de funcions és aplicat a la teoria de sèries quan la variable és natural i d’integrals
teorema de Bolzano
Matemàtiques
Teorema segons el qual una funció real de variable real s’anul·la almenys en un punt d’un interval tancat si és contínua en aquest interval i la funció pren valors de signe diferent als extrems de l’interval.
pla d’Argand-Gauss
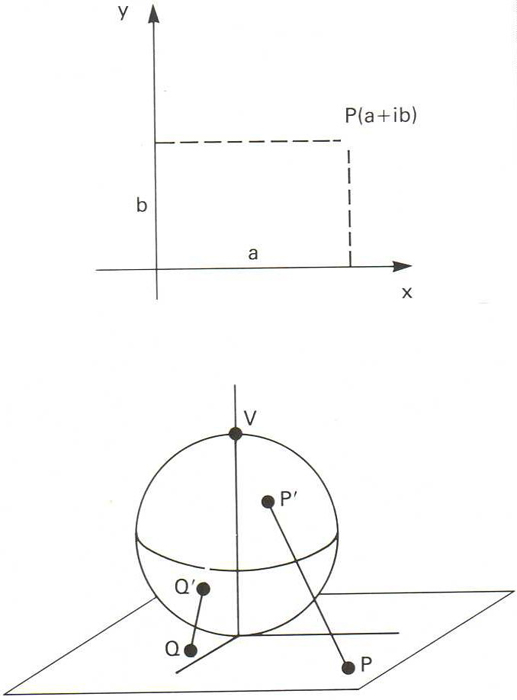
Representació del pla d’Argand-Gauss
© fototeca.cat
Matemàtiques
Pla on ha estat establert un sistema de coordenades cartesianes i en el qual és representat cada nombre complex a + bi per mitjà del punt de coordenades (a, b).
En aquesta representació tots els punts que tenen una o totes dues coordenades infinites són considerats com un mateix punt Per a fer intuïtiu el fet de considerar com un sol tots aquests punts hom utiliza la projecció estereogràfica del pla d’Argand-Gauss sobre una esfera tangent a l’origen de coordenades, de manera que tots els punts de l’infinit del pla van a parar al punt V de l’esfera
teorema de Gauss
Física
Matemàtiques
Donat un camp vectorial A, per a tota regió de l’espai de volum V limitada per una superfície S, es compleix que: ∫∫sA·dS = ∫∫∫vdivA dV.
El primer terme de l’equació és el flux de A a través de S És anomenat també teorema de la divergència o d’Ostrogadskij En el cas d’un camp elèctric E , el teorema de Gauss pren la forma q essent-hi la càrrega total dins la regió limitada per S, i ε, la constant dialèctica del medi En el cas d’un camp magnètic B , el teorema de Gauss diu cosa que implica la inseparabilitat dels pols magnètics
nombre primer de Gauss
Matemàtiques
Cadascun dels nombres primers que poden ésser expressats per la fórmula 22n + 1.
Gauss els emprà en estudiar les possibles divisions del cercle, i arribà a la conclusió que hom pot construir amb regle i compàs tot polígon regular amb un nombre primer 2 2 n + 1 de costats
mètode de racionalització de Gauss
Matemàtiques
Algorisme emprat en l’estudi dels espais vectorials que, donats uns vectors arbitraris, permet de deduir-ne efectivament els que són linealment independents i que, per tant, també són base del subespai que generen.
Hom aplica aquest mètode per a trobar el rang d’una matriu qualsevol no necessàriament quadrada, considerant cada fila de la matriu com un vector
enter de Gauss
Matemàtiques
Nombre complex de la forma a + bi, a i b essent-hi enters i .
El conjunt d’enters de Gauss, ℤ i , té estructura d’anell amb unitat