Resultats de la cerca
Es mostren 3270 resultats
esfera
Matemàtiques
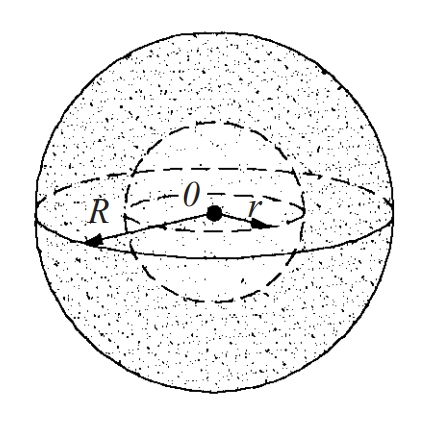
En un espai mètric de distància d, conjunt de punts x la distància dels quals a un cert punt fix p és igual a un nombre real positiu r.
El centre de l’esfera és p i el radi r , i es denota per S p r A ℝ n l’esfera de centre 0 i radi 1 es denota per S n –1 i rep el nom d’ esfera unitat
Maurits Cornelius Escher

Maurits Cornelius Escher
Hans Peters (ANEFO)
Matemàtiques
Artista neerlandès.
Creà una nombrosa collecció de dibuixos, pintures i gravats inspirats en fets matemàtics mosaics, transformacions, sanefes, perspectiva, etc, i motivà estudis matemàtics basats en la seva obra mosaics d’Escher, perspectiva curvilínia, etc Esbòs del mosaic Genets , d’ Escher
escaire
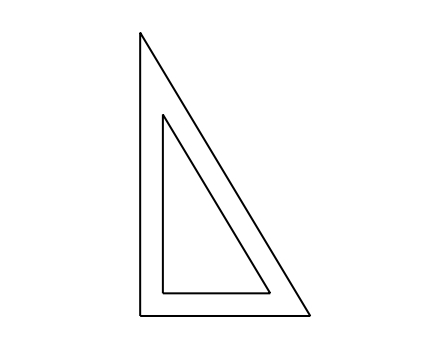
escaire
Matemàtiques
Instrument de dibuix en forma de triangle rectangle amb angles de 30°, 60° i 90°.
distància euclidiana
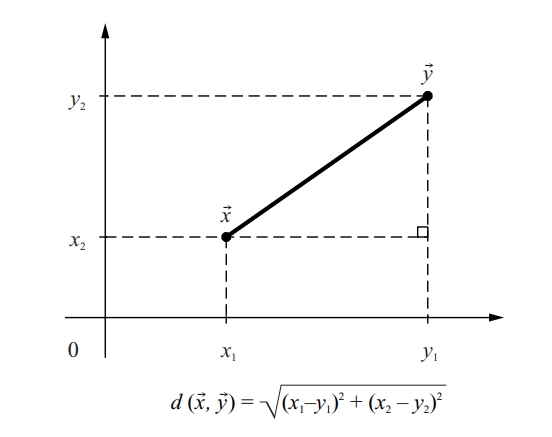
distància euclidiana
Matemàtiques
Distància definida a ℝ n.
Donats dos punts x = x 1 , , x n i y = y 1 , , y n de ℝ n , aquesta distància és definida per
cissoide de Diocles
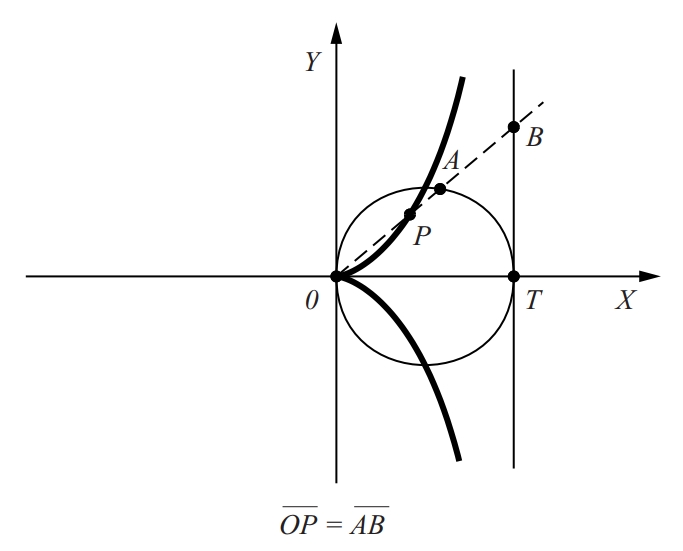
cissoide de Diocles
Matemàtiques
Cissoide associada amb una circumferència, a una recta tangent i a un punt fix O diametralment oposat al punt de tangència.
Fou construïda per Diocles per resoldre la duplicació del cub La seva equació cartesiana és y 2 2 k – x = x 3 Es tracta, doncs, d’una cúbica
dilatació
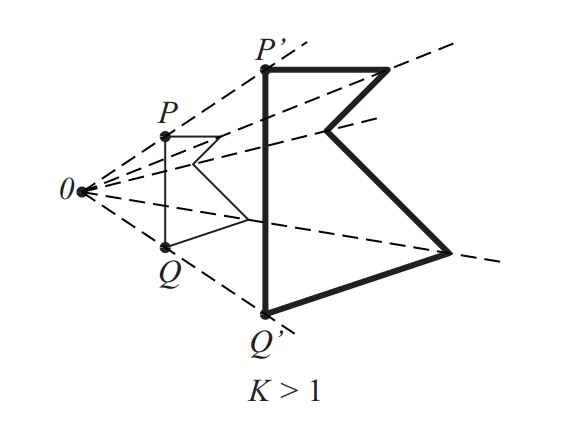
dilatació
diagrama en arbre
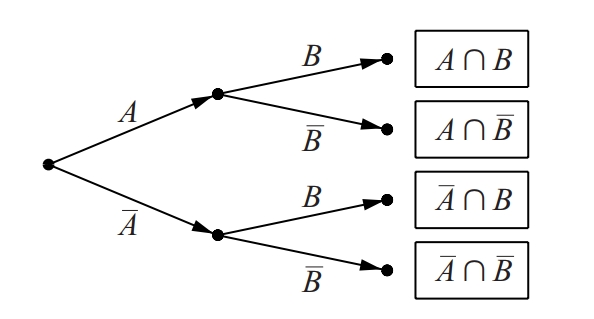
diagrama en arbre
Matemàtiques
Representació d’un sistema jeràrquic en un arbre, de manera que el grau de jerarquia s’expressa col·locant els elements en branques més o menys properes a l’arrel.
deltaedre

Els vuit deltaedres convexos
Matemàtiques
Políedre totes les cares del qual són triangles equilàters idèntics. Hi ha infinits deltaedres còncaus, però només n’hi ha vuit tipus de convexos.
digraf de De Brujin
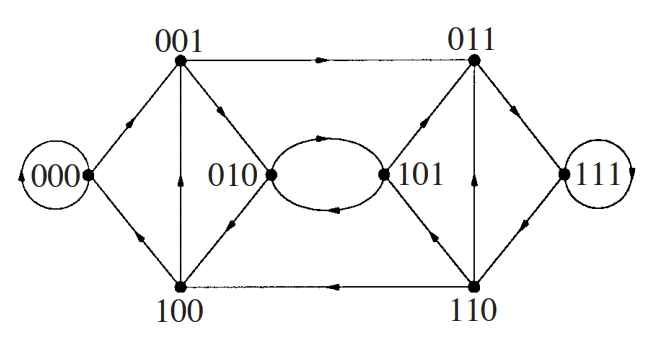
digraf de De Brujin
Matemàtiques
Digraf B(d,D) que té per conjunt de vèrtexs totes les paraules de longitud D que es poden formar amb els d símbols diferents d’un alfabet i tal que una paraula és adjacent respecte a una altra si la primera sense el símbol inicial és igual a la segona sense el símbol final.
El digraf de De Bruijn és un digraf eulerià, d -regular, que té d elevat a D + 1 arcs Els digrafs de De Bruijn són útils en el disseny de grans xarxes d’interconnexió
corona esfèrica
corona circular