Resultats de la cerca
Es mostren 3270 resultats
Abū ‘Alī al-Ḥasan ibn al-Hayṯam
Astronomia
Física
Matemàtiques
Astrònom, matemàtic i físic àrab conegut a Occident amb el nom d’Alhazen.
Es traslladà a Egipte, on proposà al califa fatimita al-Hākim un sistema per a regular les crescudes del Nil La seva obra més coneguda és el tractat d’òptica Kitāb al-manaẓir , on descriu l’ull amb una gran exactitud
derivable
Matemàtiques
Dit d’una funció que admet derivada.
Més exactament, hom parla de funció derivable a l’esquerra o derivable a la dreta en un punt si la funció té derivada a l’esquerra o a la dreta en aquest punt, respectivament Hom diu que una funció és derivable en un punt si hi és derivable a l’esquerra i a la dreta Hom parla també de funcions derivables en un interval obert o tancat f és derivable en l’interval obert a,b si és derivable en tot punt d’ell, i f és derivable en un interval tancat a,b si és derivable en a,b i ho és a la dreta de a i a l’esquerra de b
Esteve Terradas i Illa

Esteve Terradas i Illa (al centre) amb la junta de la Societat Astronòmica de Barcelona
© Fototeca.cat
Matemàtiques
Enginyer industrial i de camins i matemàtic.
Estudià a Charlottenburg Berlín, Barcelona i Madrid Es doctorà també en ciències exactes i físiques i fou professor de les universitats de Saragossa, Barcelona i Madrid S’especialitzà en ciències fisicomatemàtiques, publicà nombrosos articles sobre aquests temes i el 1909 llegí a l’Acadèmia de Ciències i Arts de Barcelona una memòria destacada Emisión de radiaciones por cuerpos fijos o en movimiento També exercí una activitat pedagògica important Publicà articles en la Revista de la Academia de Ciencias , de Madrid, i en el butlletí de l’Institut de Ciències de Barcelona Fundà un seminari…
tríedre de Frenet
Matemàtiques
Tríedre trirectangle constituït pels vectors tangent, normal i binormal a una corba en un punt.
Donada una corba C , parametritzada per l’abscissa curvilínia s s dona la longitud de l’arc des d’un punt de referència de la corba, C s = x s , y s , z s , tríede ortonormal directe definit en cada punt P de C pels vectors tangent t , normal n i binormal b , l’expressió dels quals és t = d C s / ds P , ∥ t ∥=1 n = d t / ds /∥ d t / ds ∥ P , ∥ n ∥=1 b = t ∧ n , ∥ b ∥=1 El pla P , t , n és el pla osculador de la corba C en el punt P , el pla P , n , b és el pla normal de C en P , i el pla P , b , t és el pla rectificador de C en P El radi de curvatura de C és R s = 1/∥ d t / ds…
paral·lelepípede
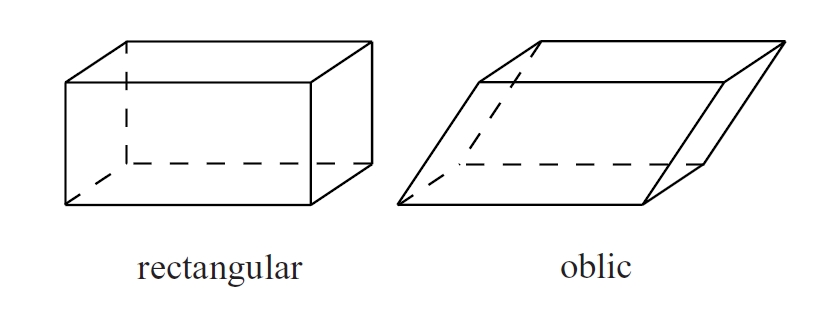
Paral·lelepípede
Matemàtiques
Prisma de sis cares, totes elles paral·lelograms.
Quan el prisma és recte i totes les cares són rectangles, és anomenat ortòedre L’ hexàedre és l’únic parallelepípede que és políedre regular
ortòedre
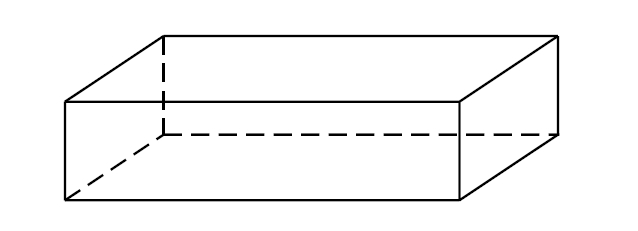
Ortòedre
Matemàtiques
Prisma de sis cares rectangulars que té tots els angles rectes.
Si les longituds de les arestes són a, b i c , la fórmula del volum de l’ortòedre és V=abc
icosàedre
Matemàtiques
Políedre de vint cares, trenta arestes i dotze vèrtexs.
En l’ icosàedre regular les cares són triangles equilàters iguals
flexàedre
Matemàtiques
Políedre flexible de cares rígides.
Els flexàedres han de tenir necessàriament més de set vèrtexs, i hom n’ha construït de nou vèrtexs i de més
cubooctàedre
Matemàtiques
Cos que resulta de tallar els vuit angles sòlids d’un cub de manera que en resulta un políedre que té vuit cares que són triangles equilàters i sis cares quadrades.