Resultats de la cerca
Es mostren 29 resultats
Leonhard Euler
Matemàtiques
Matemàtic suís.
Deixeble de JBernoulli a la Universitat de Basilea, fou professor de física 1730 i de matemàtiques 1733 a l’Acadèmia de Ciències de Rússia a Peterburg Nomenat, per Frederic el Gran, director de la secció de matemàtiques de l’Acadèmia de Ciències de Berlín, Caterina II el nomenà director de l’Acadèmia de Peterburg 1766 Fou membre de la Royal Society 1746 i de l’Académie Française des Sciences 1755 Estudià les sèries algèbriques i demostrà que només poden ésser emprades quan són convergents Introduí la notació f x , el nombre π, el nombre e com a base de logaritmes, la i per a representar la…
indicador d’Euler
Matemàtiques
Donat un nombre natural no nul, n ≥2, nombre ϕ(n) que indica quants nombres primers amb n i inferiors a n hi ha.
És donat per l’expressió ϕ n = n 1-1/ p 1 1-1/ p 2 1-1/ p n , on n = p 1 a 1 p 2 a 2 p n a n , és la descomposició de n en factors primers descomposició en factors primers a ℤ
constant d’Euler
Matemàtiques
Límit quan n →∞; de la sèrie {un}, n>0, de terme general un= 1+1/2+1/3+...+ 1/n-ln n.
El seu valor aproximat és C = 0,577 215 66
diagrama d’Euler-Venn
Matemàtiques
Representació gràfica d’un conjunt o d’una operació entre conjunts.
teorema de la recta d’Euler
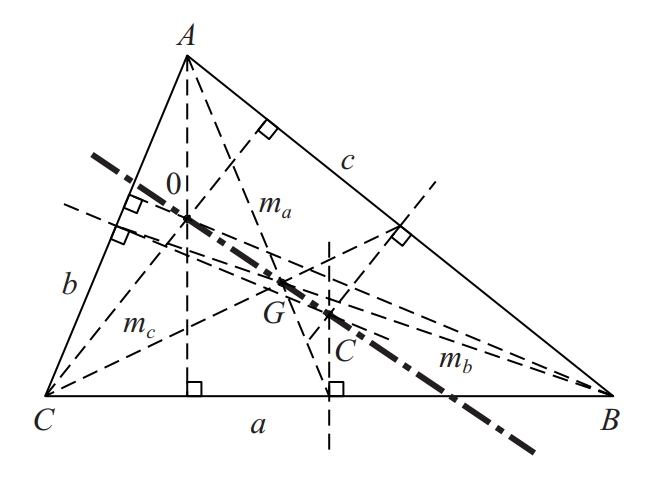
teorema de la recta d’Euler
Matemàtiques
Resultat que prova que l’ortocentre, el circumcentre i el baricentre d’un triangle estan alineats i que el baricentre és a una distància doble de l’ortocentre que del circumcentre.
La recta que passa per aquests punts s’anomena recta d’Euler
funció beta
Matemàtiques
Funció definida per l’equació
que convergeix per a valors de r i s positius.
Anomenada també primera integral d’Euler, és relacionada amb la segona integral d’Euler funció gamma per l’equació
pi
Matemàtiques
Lletra grega, inicial del mot grec περιφέρεια (‘circumferència’)..
És adoptada per a representar la raó constant que existeix entre la longitud de la circumferència i el seu diàmetre longitud de la circumferència, 2πR àrea del cercle, πR 2 àrea de l’esfera, 4πR 2 volum de l’esfera, L’ús d’aquesta llegra grega per a designar la relació entre la longitud de la circumferència i el seu diàmetre es remunta solament al s XVII, i es generalitzà a partir de la publicació de l’obra d’Euler Introductio in analysim infinitorum el mateix Euler i JBernoulli usaren P i c , respectivament, com a símbol representatiu A Egipte hom havia fet…
teorema de Fermat
Matemàtiques
Teorema segons el qual si p és un nombre primer i a un nombre primer amb p, aleshores es satisfà que ap-1—1 és divisible per p, o sigui, ap-1≡(mod p).
La primera demostració d’aquest teorema fou feta per Euler el 1736
Johann Bernoulli
Matemàtiques
Matemàtic suís.
Començà estudiant medicina, però es decantà molt aviat per les matemàtiques Fou deixeble del seu germà Jakob, que l’inicià en l’obra de Leibniz, de la qual fou propagador Estigué a París 1690-95, on redactà un curs de càlcul per al marquès de L’Hôpital hom creu que la coneguda regla de L’Hôpital és deguda a Johann Bernoulli El 1691 determinà les tangents i els radis de curvatura de moltes corbes planes i donà el primer exemple de coordenades polars Fou professor a Groningen 1695-1705 i, des de la mort del seu germà Jakob, a Basilea 1705, on fou mestre d’Euler Proposà i resolgué…
factorial
Matemàtiques
Producte dels nombres naturals consecutius, des de l’1 fins al nombre del qual hom calcula el factorial.
És indicat per n La generalització de la noció de factorial a nombres no naturals és possible mitjançant la funció Γ d’Euler gamma Per a molt gran, hom pot calcular n aproximadament per mitjà de la fórmula de Stirling