Resultats de la cerca
Es mostren 122 resultats
rodolament
Matemàtiques
Desplaçament d’una corba, anomenada rodolant, sobre una altra corba fixa, anomenada base, de manera que ambdues restin constantment tangents i que el punt de contacte recorri alhora arcs iguals sobre les dues corbes.
La trajectòria descrita per un punt de la corba mòbil és anomenada ruleta
ruleta
Matemàtiques
Trajectòria descrita per un punt d’una corba, anomenada rodolant, que rodola sobre una altra anomenada base (rodolament).
Els exemples més coneguts són els de les corbes anomenades cicloide, epicicloide i hipocicloide
adjacent
Matemàtiques
En un graf (o digraf), dit dels vèrtexs comunicats per una aresta (anomenada arc).
Es diu que els digrafs són adjacents des de o adjacents cap a per a indicar el sentit de l’arc
envolupant
Matemàtiques
Corba tangent a totes les d’una família, cadascuna de les quals és anomenada involuta
.
Donada la família de corbes f x,y,h = 0, hom calcula l’equació de l’envolupament eliminant el paràmetre h entre l’equació de la família f x,y,h = 0 i la derivada respecte a h, f' h x,y,h = 0 El concepte d’envolupant també pot ésser aplicat a una família de superfícies
binomi de Newton
Matemàtiques
Fórmula per a calcular la potència enèsima d’un binomi, anomenada també teorema del binomi.
En el cas que l’exponent n del binomi sigui un nombre natural, la fórmula pot ésser demostrada per inducció, i la seva expressió és on els coeficients n k , anomenats coeficients binomials , són donats per la fórmula Aquesta expressió, que ja utilitzà NTartaglia, fou ampliada per INewton en el cas d’exponents negatius i fraccionaris i per LEuler en el cas d’exponents irracionals En el cas, però, que l’exponent n no sigui un nombre natural, l’anterior expressió esdevé una sèrie infinita i, per tant, només té sentit quan la sèrie és convergent, cosa que imposa certes limitacions als valors de…
fracció periòdica
Matemàtiques
Fracció l’expressió decimal de la qual conté una xifra o grup de xifres (anomenades període) que es repeteixen indefinidament.
P ex, el període d’1/3 = 0,333 és 3, el d’1/6 = 0,1666 és 6 Quan el període comença a les dècimes, la fracció és anomenada periòdica pura en la resta de casos és anomenada periòdica mixta
superfície de revolució
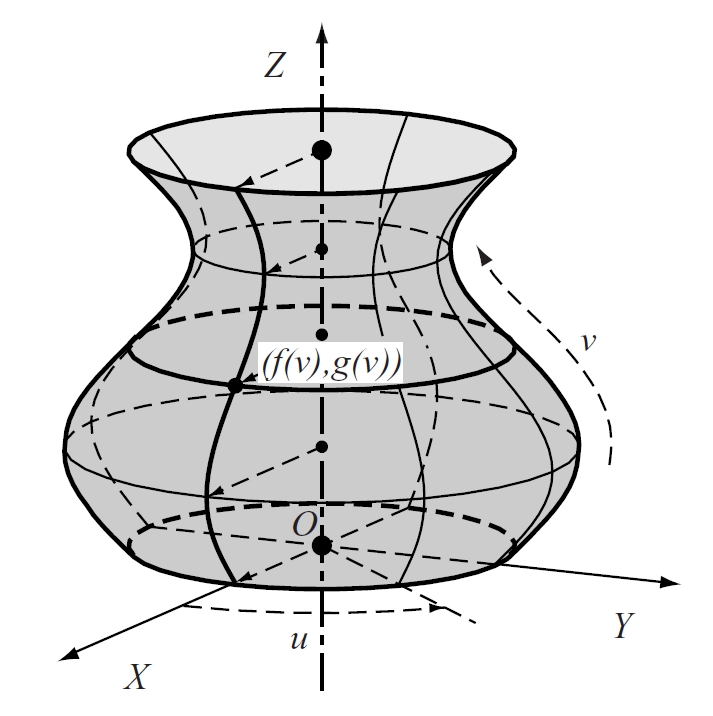
Superfície de revolució
Matemàtiques
Superfície engendrada per la rotació d’una corba (generatriu) entorn d’un eix, anomenat de revolució.
Si aquesta corba és plana i situada en un pla que conté l’eix és anomenada meridiana de la superfície La circumferència descrita per cada punt de la meridiana és anomenada parallel Els meridians i els parallels d’una superfície esfèrica són circumferències Els meridians de la superfície terrestre són aproximadament ellipses
singular
Matemàtiques
Dit de la solució d’una equació diferencial que no és deduïble de l’anomenada solució general
.
hèlix
Matemàtiques
Corba guerxa tal que la seva tangent forma un angle constant amb una recta fixa anomenada eix
.
Las més coneguda és l' hèlix circular , que hom obté en combinar un moviment circular uniforme entorn d’un eix amb un moviment uniforme parallel a l’eix
forma
Matemàtiques
Aplicació f d’un espai vectorial E de n dimensions en el cos K d’escalars en el qual és definit i que generalment és el cos dels nombres reals o dels nombres complexos.
Segons quin sigui el valor de n i les propietats de f , hom distingeix diversos tipus de formes Hom diu que f és una forma lineal o funcional lineal si, per a x i y de E i λ de K, f satisfà f x+y = f x + f y i f λ x = λ f x El conjunt de formes lineals d’un espai vectorial E sobre el seu K , és E* , espai dual Si hom pot considerar E com a producte cartesià de n espais vectorials, una forma f transforma tot conjunt ordenat de n vectors en un escalar de K si aquesta f , en ésser restringida a un vector qualsevol, constitueix una forma lineal, f és anomenada forma…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina