Resultats de la cerca
Es mostren 22 resultats
arcs suplementaris
Matemàtiques
Arcs circulars d’una circumferència que, reunits, formen una semicircumferència i que corresponen a angles suplementaris.
arcs conjugats
Matemàtiques
Parella d’arcs circulars d’una circumferència sense punts interiors en comú i que, reunits, formen aquesta circumferència.
arcs congruents
Matemàtiques
Arcs circulars entre els quals es pot establir un moviment rígid o isometria que transformi l’un en l’altre.
arcs complementaris
Matemàtiques
Arcs circulars d’una mateixa circumferència la llargada total dels quals és un quart del perímetre de la circumferència i que correspon a angles complementaris.
graf
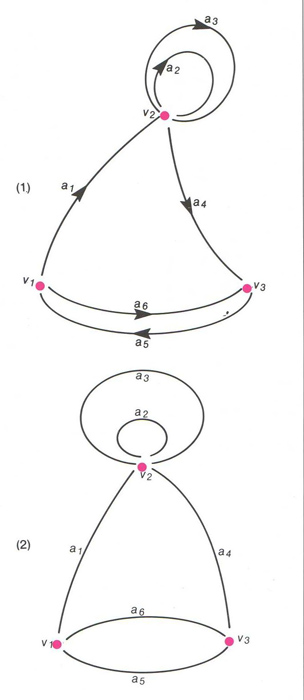
(1) Graf orientat: el camí ( a 1, a 2, a 4, a 5) és un circuit , els arcs a 2 i a 3 són bucles o rulls en el vèrtex v 2. i a 6 és un camí de v 1 a v 3. (2) graf no orientat: la cadena ( a 1, a 4, a 5) és un cicle , les arestes a 2 i a 3 són bucles o rulls en el vèrtex v 2, i a 6 és una aresta de v 1 a v 3.
© fototeca.cat
Matemàtiques
Ens constituït per un conjunt S
d’elements i per un conjunt C
de línies que uneixen els elements de S
(tot palesant una correspondència
de S
en si mateix).
Cal distingir entre un graf orientat i un graf no orientat Un graf orientat és una quaterna S, C, o, e , on S és el conjunt d’elements o vèrtexs, C és el conjunt de línies entre els vèrtexs o arcs, o és l' aplicació origen que assigna a cada arc el vèrtex del qual surt, i e és l' aplicació extrem que assigna a cada arc el vèrtex al qual arriba Un graf no orientat és una terna S, C, e , on S és el conjunt dels vèrtexs, C és el conjunt de línies entre els vèrtexs o arestes , i e és l’aplicació que assigna a cada aresta una parella de S × S , formada pels vèrtexs que uneix l’…
digraf
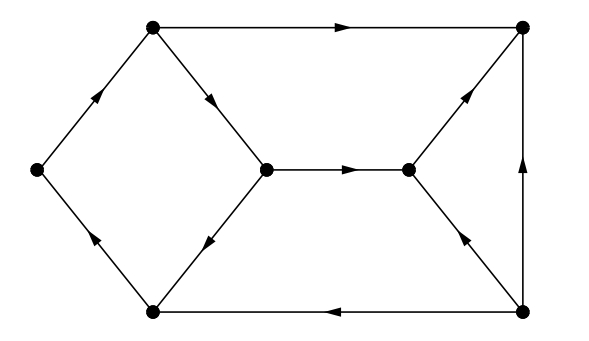
digraf
Matemàtiques
Graf les arestes del qual, anomenades arcs, són parells ordenats de vèrtexs diferents.
Un digraf G amb un conjunt de vèrtexs V i un conjunt d’arcs E es denota per G = V , E Sovint s’escriu també E = E G i V = V G
regla de Simpson
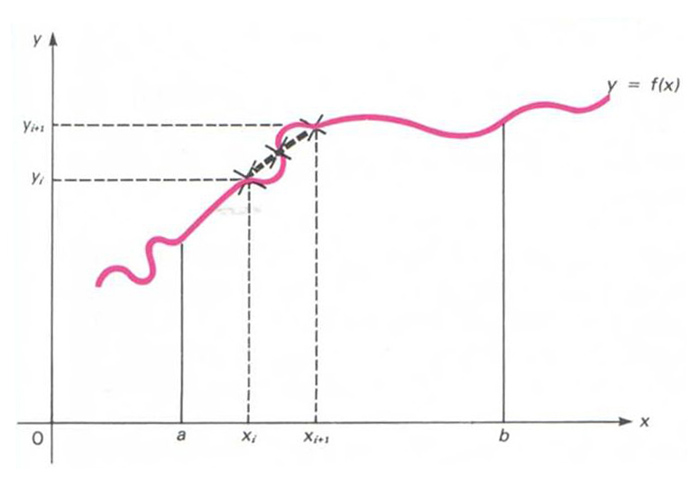
Regla de Simpson
© fototeca.cat
Matemàtiques
Mètode per a aproximar l’àrea limitada per una corba y = f(x), l’eix OX i dues rectes paral·leles x = a i x = b.
El mètode suposa que els petits arcs de la corba són aproximables mitjançant arcs de paràbola que passen pel punt mitjà i pels punts terminals de l’arc considerat La fórmula que hom obté amb aquesta aproximació és usant les sèries de Taylor fins als termes quadràtics on l’interval a,b ha estat dividit en 2 n subintervals a, x 1 , x 2 , , x 2 n - 1 , b , i y a , y 1 , y 2 , , y 2 n - 1 , y b són les respectives ordenades d’aquests punts, y i = f x i La diferència numèrica entre l’àrea real i aquesta àrea aproximativa A , és fitada per la quantitat M b-a 5 /…
angle exterior a una circumferència
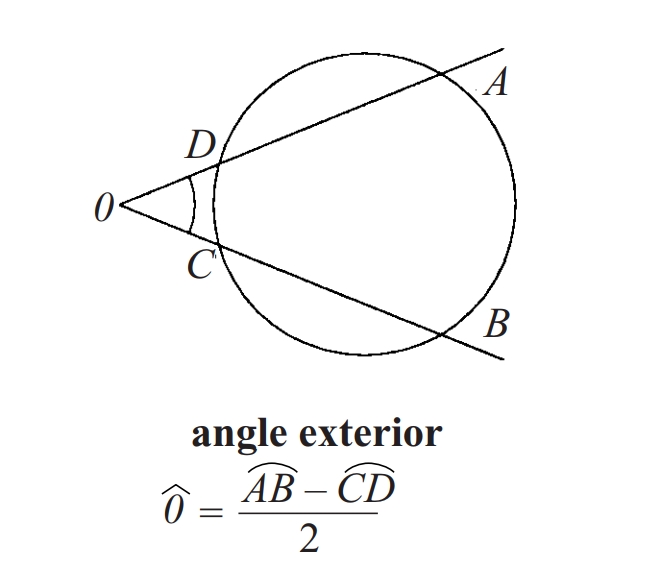
angle exterior
Matemàtiques
Angle el vèrtex del qual és un punt exterior a una circumferència i els costats són dues rectes secants a la circumferència.
Mesura la meitat de la diferència entre els dos arcs subtendits
polígon esfèric
Matemàtiques
Porció de la superfície d’una esfera que és limitada per arcs de cercles màxims.