Resultats de la cerca
Es mostren 5 resultats
asímptota
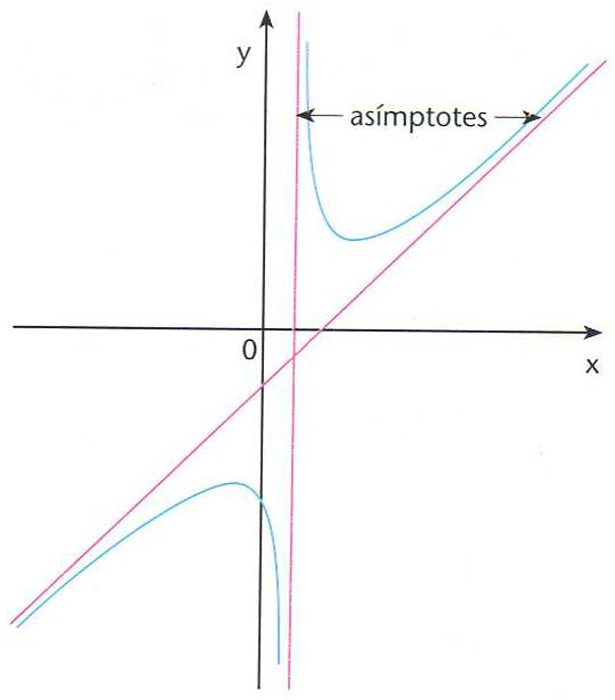
Asímptotes
Matemàtiques
Recta a la qual s’acosta un punt variable sobre una branca de corba quan el punt s’allunya cap a l’infinit.
Per a poder afirmar que una branca de corba té una asímptota cal que, si el punt P es mou sobre aquesta de manera que la distància de P a l’origen de coordenades O creix infinitament, la direcció de la recta OP tingui un límit determinat Hom troba aquest límit per mitjà del quocient y/x = tg a Coneguda la direcció de l’asímptota, hom determina la seva ordenada a l’origen per la condició que la distància entre dos punts que tinguin igual abscissa, un sobre la corba, l’altre sobre l’asímptota, tingui límit zero quan aquella abscissa comuna es fa infinita Així, per exemple, la hipèrbola té dues…
foli de Descartes
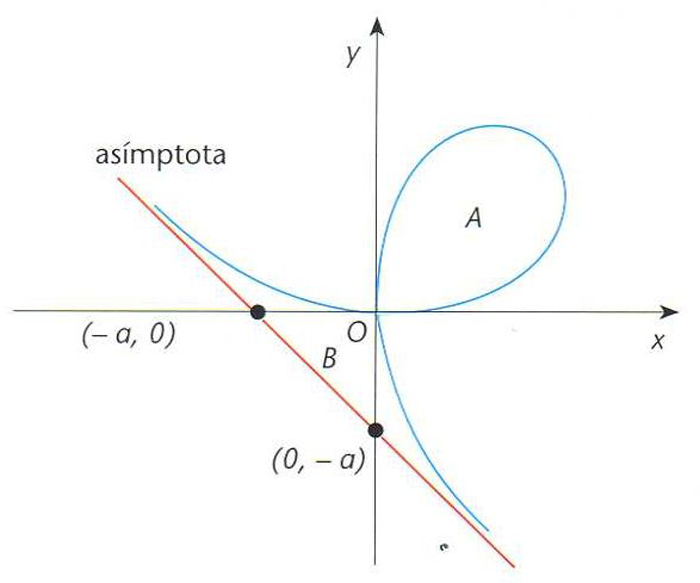
Foli de Descartes
© fototeca.cat
Matemàtiques
Cúbica expressada implícitament per l’equació cartesiana x3+y3=3axy, on a és una constant.
En forma paramètrica és expressada per x=3at|1+t 3 i y=3at 2 |1+t 3 La recta traçada pels punts de coordenades - a , 0 i 0, -a és una asímptota de la corba L’àrea A limitada pel llaç és igual a l’àrea B compresa entre les dues branques infinites i la asímptota esmentada
estrofoide
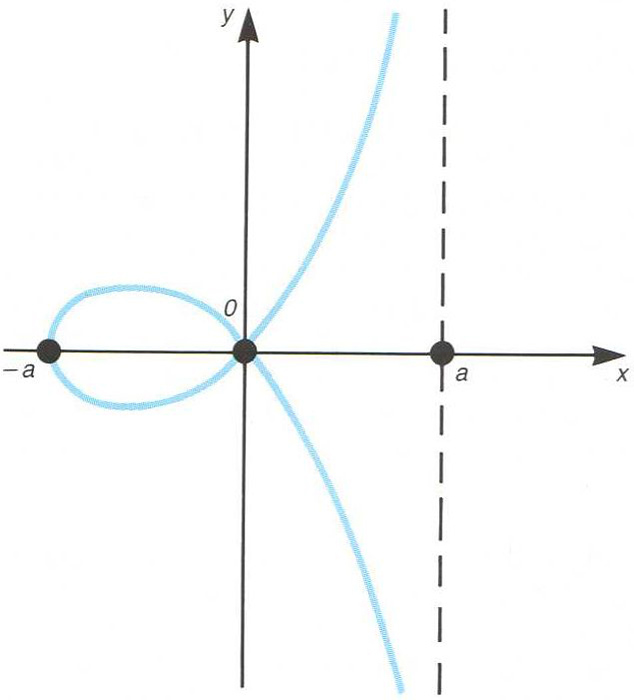
Estrofoide
© fototeca.cat
Matemàtiques
Corba plana, cúbica circular d’equació cartesiana
y 2
( a-x
) =
x 2
( a+x
), a
>0.
L’origen és un punt doble L’equació en coordenades polars és r = - a cos 2ϑ/cos ϑ La línia x = a n'és una asímptota
hipèrbole
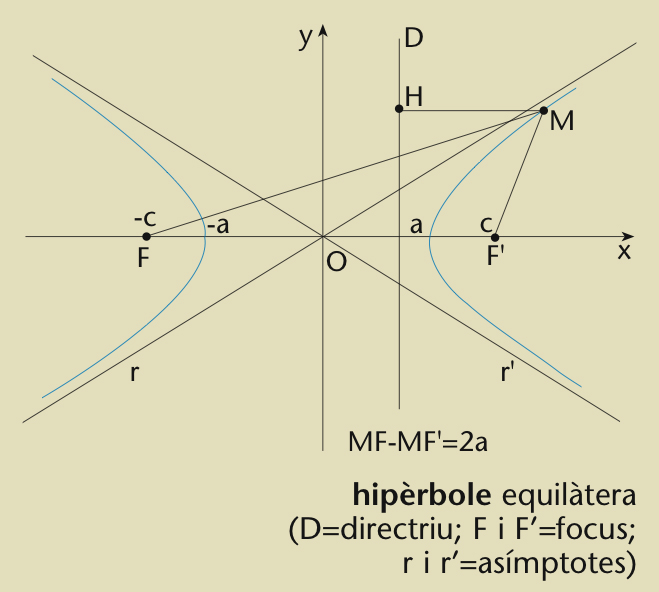
Hipèrbole equilàtera
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’un con de revolució amb un pla que forma amb ’eix d’aquell un angle més petit que amb la generatriu.
Constitueix el lloc geomètric dels punts del pla tals que la diferència de llurs distàncies a dos punts fixos, anomenats focus , és una constant, simbolitzada habitualment per 2 a Té dos eixos de simetria i, referida a ells, la seva equació és x 2 / a 2 - y 2 / b 2 = 1, on i 2c és la distància entre els focus L’excentricitat e és c / a Les asímptotes són les rectes y = b / a x asímptota Quan a = b , la hipèrbola és anomenada equilàtera , i la seva equació referida a les asímptotes, que són perpendiculars, és y = k/ x la seva excentricitat és