Resultats de la cerca
Es mostren 19 resultats
conjunt ben ordenat
Matemàtiques
Conjunt ordenat en el qual tot subconjunt no buit té un primer element.
Conjunt ordenat OOO X ,≤OOO si, i només si, tot subconjunt Y ⊆ X , no buit, té primer element Els nombres ordinals mesuren precisament les diferents menes de bons ordres possibles És a dir, tot conjunt ben ordenat és ordre-isomorf a un únic nombre ordinal
Yĕhudà ben Verga
Astronomia
Historiografia
Matemàtiques
Historiador, matemàtic i astrònom jueu.
Acusat davant la inquisició, hagué d’exiliar-se a Portugal, on morí a la presó inquisitorial És l’iniciador de l’obra històrica Šebet Yĕhudà ‘La vara de Judà’, continuada pel seu descendent Šĕlomó ibn Verga
Leví ben Geršom
Astronomia
Filosofia
Matemàtiques
Metge, matemàtic, astrònom, filòsof i exegeta.
Tingut per heterodox, fou el pensador més original del judaisme medieval, després de Maimònides Escriví cinc llibres de matemàtiques i un de lògica i fou un dels primers a escriure sobre trigonometria plana En astronomia enginyà nous aparells, als quals dedicà un poema Comentarista del Pentateuc i d’una dotzena més de llibres bíblics, de la Isagoge de Porfiri i d’obres d’Aristòtil, a la seva obra principal, Milḥamot Adonay ‘Les guerres del Senyor’, sobre la filosofia de la religió, s’inclina vers l’aristotelisme
Iṣḥaq ben Mošé Elí ha-Sefardí
Literatura
Matemàtiques
Judaisme
Autor jueu del qual es conserven, en hebreu, escrits després de l’expulsió de l’any 1492, dos llibres de matemàtiques elementals.
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…
àlef
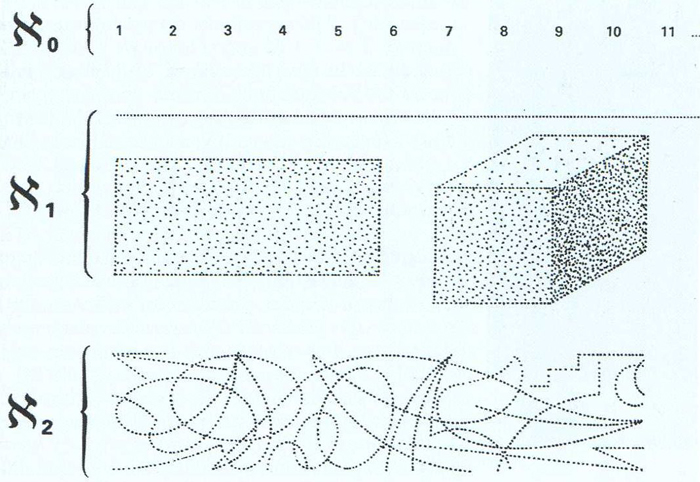
Comparació del cardinal dels naturals, ℵ0, amb els cardinals estrictament més grans: ℵ1, cardinal del continu, i ℵ2, cardinal de les corbes del pla
© Fototeca.cat
Escriptura i paleografia
Matemàtiques
Símbol ℵ que designa el cardinal dels conjunts infinits ben ordenats.
Acompanyat pel subíndex zero indica la classe dels conjunts infinits numerables, que permeten d’establir una correspondència biunívoca amb els nombres naturals, 1, 2, 3, Per exemple, el conjunt dels nombres parells té cardinal, ja que a cada nombre parell 2n hom pot fer correspondre la seva meitat n
definició per recurrència
Matemàtiques
Definició d’una funció sobre els nombres naturals definint-la per a 1 i, per a cada n més gran que 1, en funció dels valors que pren per a nombres més petits que n
.
Per exemple, la funció factorial pot ésser definida fent 1 = 1 i, per a un n > 1, fent n = n -1 n Aquests procediments de demostració i de definició, ja coneguts i emprats pels grecs, han estat generalitzats i ara hom utilitza les recurrències a qualsevol conjunt ben ordenat on tot subconjunt té mínim Aleshores, per a demostrar que una proposició és veritable per a tot element del conjunt ben ordenat, basta demostrar que és veritable per a tot element si ja ho és per a tots els anteriors
aberrància
Matemàtiques
Singularitat que es presenta quan els valors obtinguts d’un conjunt d’observacions d’una magnitud disten ostensiblement del valor mitjà obtingut amb totes les observacions.
Aquest terme és aplicat quan un nombre reduït de diversos fets presenten d’una manera excepcional unes característiques diferents d’altres fets que, dins el mateix cas, són relativament ben agrupats al voltant d’un valor mitjà