Resultats de la cerca
Es mostren 5 resultats
nombres conjugats
Matemàtiques
Dit de dos nombres algèbrics sobre un camp donat si són arrels de la mateixa equació irreductible amb coeficients en el camp.
Així, els nombres complexos a + bi, a-bi són conjugats sobre el camp real, puix que són arrels de l’equació X 2 - 2aX + a 2 + b 2 = 0
nombre complex
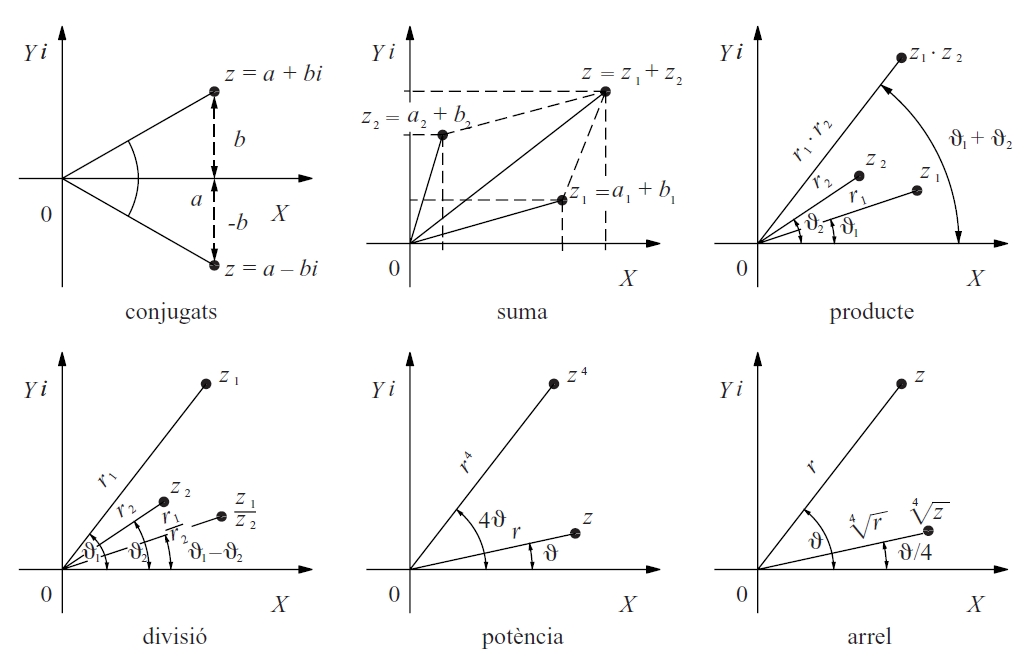
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-Gauss Aquesta…
enter de Gauss
Matemàtiques
Nombre complex de la forma a + bi, a i b essent-hi enters i .
El conjunt d’enters de Gauss, ℤ i , té estructura d’anell amb unitat
pla d’Argand-Gauss
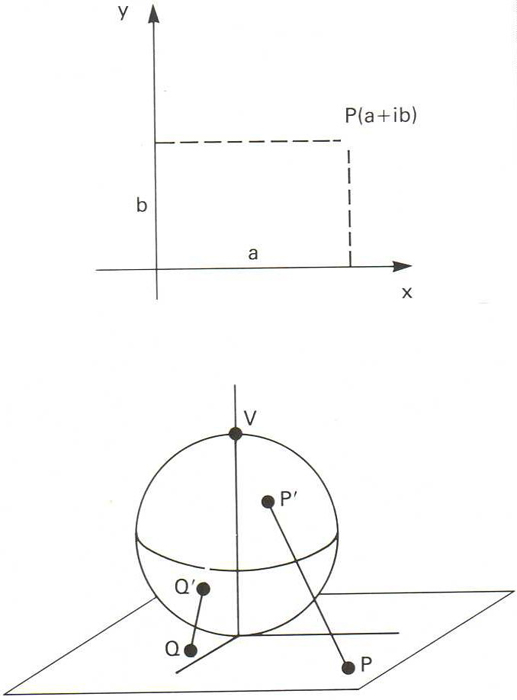
Representació del pla d’Argand-Gauss
© fototeca.cat
Matemàtiques
Pla on ha estat establert un sistema de coordenades cartesianes i en el qual és representat cada nombre complex a + bi per mitjà del punt de coordenades (a, b).
En aquesta representació tots els punts que tenen una o totes dues coordenades infinites són considerats com un mateix punt Per a fer intuïtiu el fet de considerar com un sol tots aquests punts hom utiliza la projecció estereogràfica del pla d’Argand-Gauss sobre una esfera tangent a l’origen de coordenades, de manera que tots els punts de l’infinit del pla van a parar al punt V de l’esfera
quaternió
Matemàtiques
Símbol del tipus a +bi + cj +dk, on a, b, c, d són nombres reals i i, j, k segueixen les regles formals algèbriques: i2 = j2 = k2 = -1, i · j =-j · i =k, j k = -k . j = i, k . i =-i · k = j
.
Els quaternions poden ésser operats algèbricament suma i producte, com els complexos, dels quals són una extensió El conjunt dels quaternions té estructura de cos no commutatiu Els quaternions foren introduïts i estudiats per WRHamilton