Resultats de la cerca
Es mostren 20 resultats
Georg Ferdinand Frobenius
Matemàtiques
Matemàtic alemany.
Fou professor a la Universitat de Berlín Investigà en les branques més elevades de l’àlgebra, en connexió amb la teoria de les funcions i dels grups Els nombrosos teoremes que duen el seu nom representen un enriquiment de l’àlgebra clàssica i constitueixen un dels punts de partida de l’àlgebra moderna
foli de Descartes
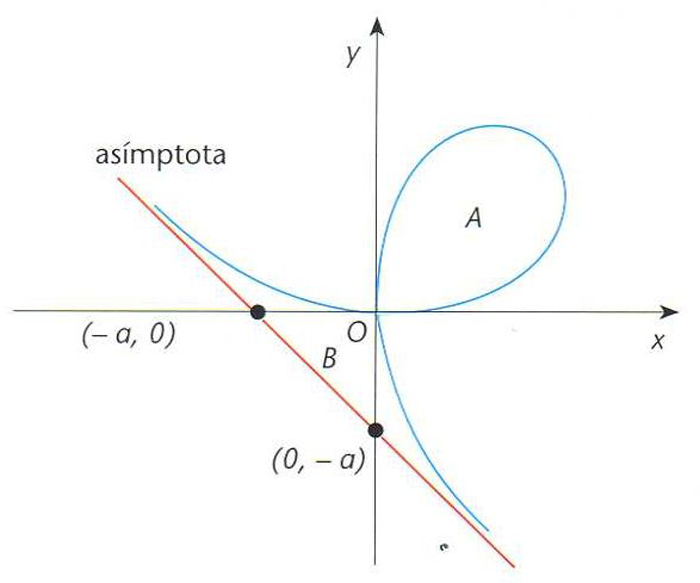
Foli de Descartes
© fototeca.cat
Matemàtiques
Cúbica expressada implícitament per l’equació cartesiana x3+y3=3axy, on a és una constant.
En forma paramètrica és expressada per x=3at|1+t 3 i y=3at 2 |1+t 3 La recta traçada pels punts de coordenades - a , 0 i 0, -a és una asímptota de la corba L’àrea A limitada pel llaç és igual a l’àrea B compresa entre les dues branques infinites i la asímptota esmentada
Garrett Birkhoff

Garrett Birkhoff
Matemàtiques
Matemàtic i físic nord-americà.
A partir dels anys trenta inicià l’estudi de diverses branques de l’àlgebra moderna que conduïren a la creació de l’àlgebra universal Estudià algebres lliures, teoremes d’isomorfisme i d’homomorfisme, reticles de congruències, reticles en general, sistemes equacionals, etc També cal remarcar les seves contribucions en mecànica de fluids, anàlisi numèrica i teoria nuclear
Marie-Joseph Kampé de Fériet
Matemàtiques
Matemàtica francesa.
Contribuí a crear i desenvolupar moltes de les branques de la matemàtica pura i aplicada Foren transcendents les seves aportacions a la mecànica de fluids, anàlisi, probabilitat, teoria de les equacions funcionals, teoria generalitzada de la informació, etc Fou investida doctora honoris causa a les universitats de Gant i Bolonya, i nomenada membre de les acadèmies de ciències de París, Madrid, Varsòvia, Washington i Nova York
Peter Gustav Lejeune Dirichlet

Peter Gustav Lejeune Dirichlet
© Fototeca.cat
Matemàtiques
Matemàtic alemany.
El 1855 succeí Gauss en la càtedra de matemàtiques de la Universitat de Göttingen Féu notables contribucions a moltes branques de la matemàtica i de la física matemàtica En el camp de l’anàlisi establí les condicions generals perquè una funció sigui expressable per mitjà de sèries trigonomètriques, i estudià les sèries que duen el seu nom i les integrals numèriques els treballs sobre les sèries de Fourier el portaren a donar una definició completament general de funció numèrica 1829 El seus estudis sobre l’equilibri de sistemes i la teoria del potencial el dugueren a formular el…
concoide d’una corba respecte a un punt
Matemàtiques
Donada una corba C
i un punt O
del seu pla, lloc geomètric dels punts Q
i Q’
determinats en mesurar, a ambdós costats, una determinada distància b
a partir del punt P
obtingut en tallar la corba C
mitjançant una recta R
que passi per O
.
De la definició resulta palès que la concoide d’una corba té dues branques Si C és una recta, i hom escull un sistema de coordenades polars amb origen al punt O , separat de C per una distància perpendicular a , l’expressió de la concoide de la recta C respecte a O és r= a/cos θ+ b si a < b es determina un llaç en O , si a = b hi ha una cúspide en O i la concoide és la concoide de Nicomedes , i si a > b no hi ha cúspide però hi ha un acnode en O Un altre cas particular s’escau quan C és una circumferència en aquest cas, la concoide de la circumferència C respecte a un…
Israil Moisejevič Gelfand
Biologia
Matemàtiques
Matemàtic i biòleg ucraïnès.
Estudià amb AN Kolmogorov Els seus treballs sobre espais lineals normals han estat el fonament d’aplicacions en anàlisi funcional de diverses branques matemàtiques Professor a l’Acadèmia de Ciències de l’URSS 1935-41 i des d’aquest any de la Universitat Estatal de Moscou, el 1960 fundà l’Institut de Física Biològica i, basant-se en aplicacions matemàtiques, emprengué recerques en el camp de la fisiologia cellular És autor de Funcions automòrfiques i la teoria de les representacions 1962 i de Mecanismes de morfogènesi a les estructures cellulars 1977, entre d’altres En 1989-90…
arbre
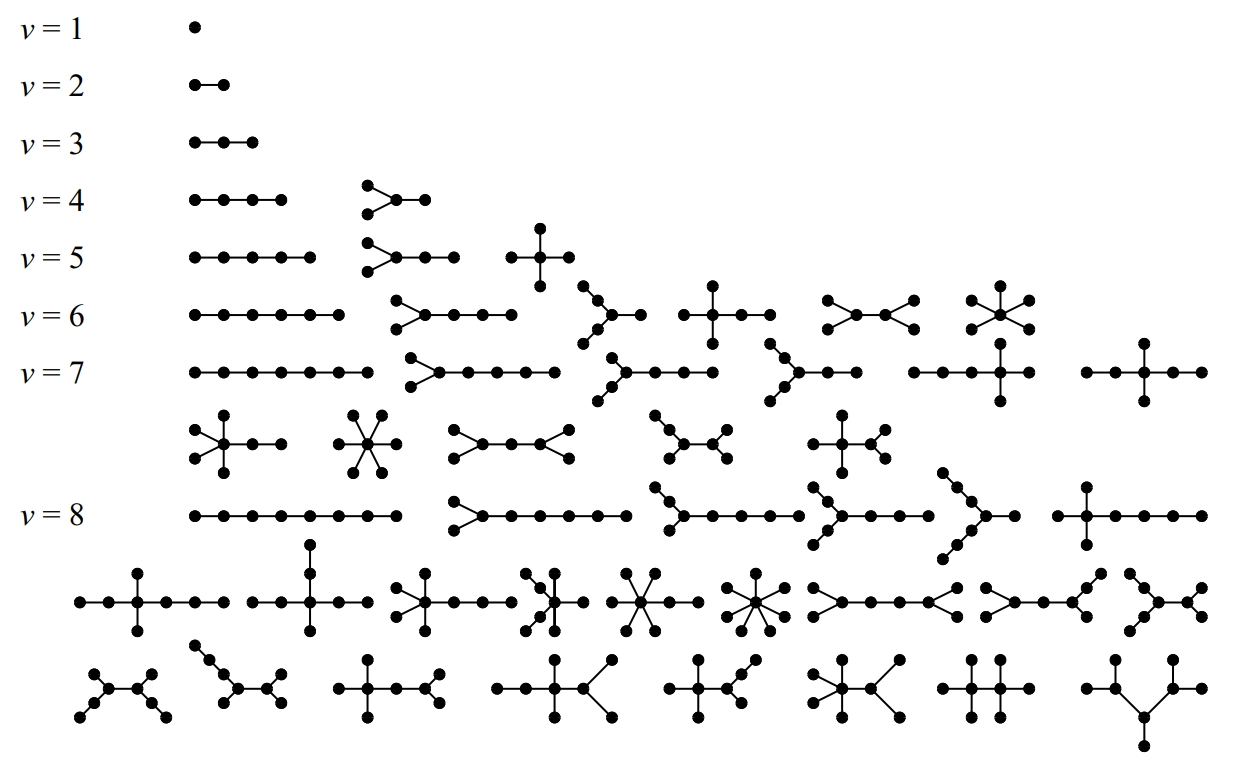
Tots els arbres amb vuit vèrtexs com a màxim
© fototeca.cat
Matemàtiques
Graf connex i acíclic (sense circuits).
Un arbre té només un vèrtex, anomenat arrel sense predecessor en el sentit de les fletxes, mentre que tot altre vèrtex té, cada un, un únic predecessor Tots els vèrtexs tenen un nombre variable de successors, que ordinariàment hom suposa ordenats per exemple, d’esquerra a dreta i de vegades són anomenats branques En la representació habitual d’un arbre l’arrel se situa al capdamunt i els arcs se suposen recorreguts en sentit descendent Els arbres han passat d’ésser un cas particular de graf a rebre un tractament matemàtic específic Són particularment útils en la modelització de…