Resultats de la cerca
Es mostren 439 resultats
cònica
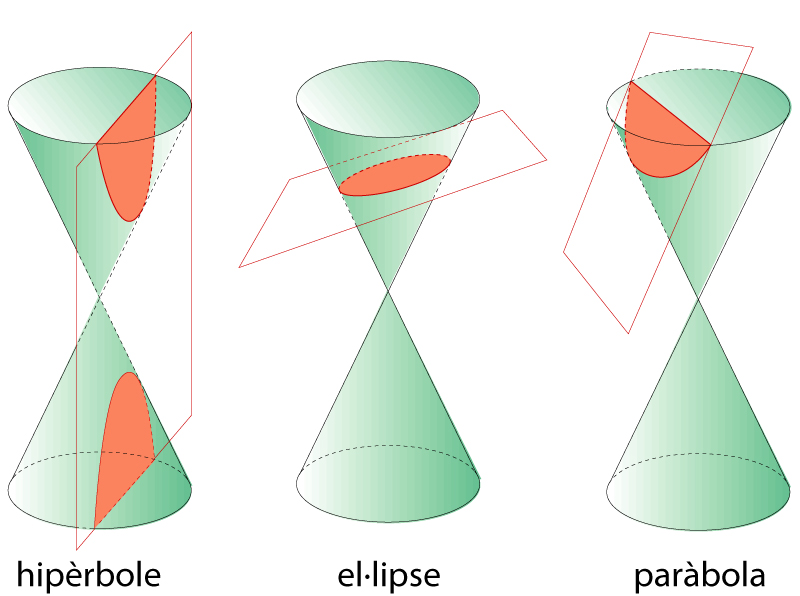
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…
arbre
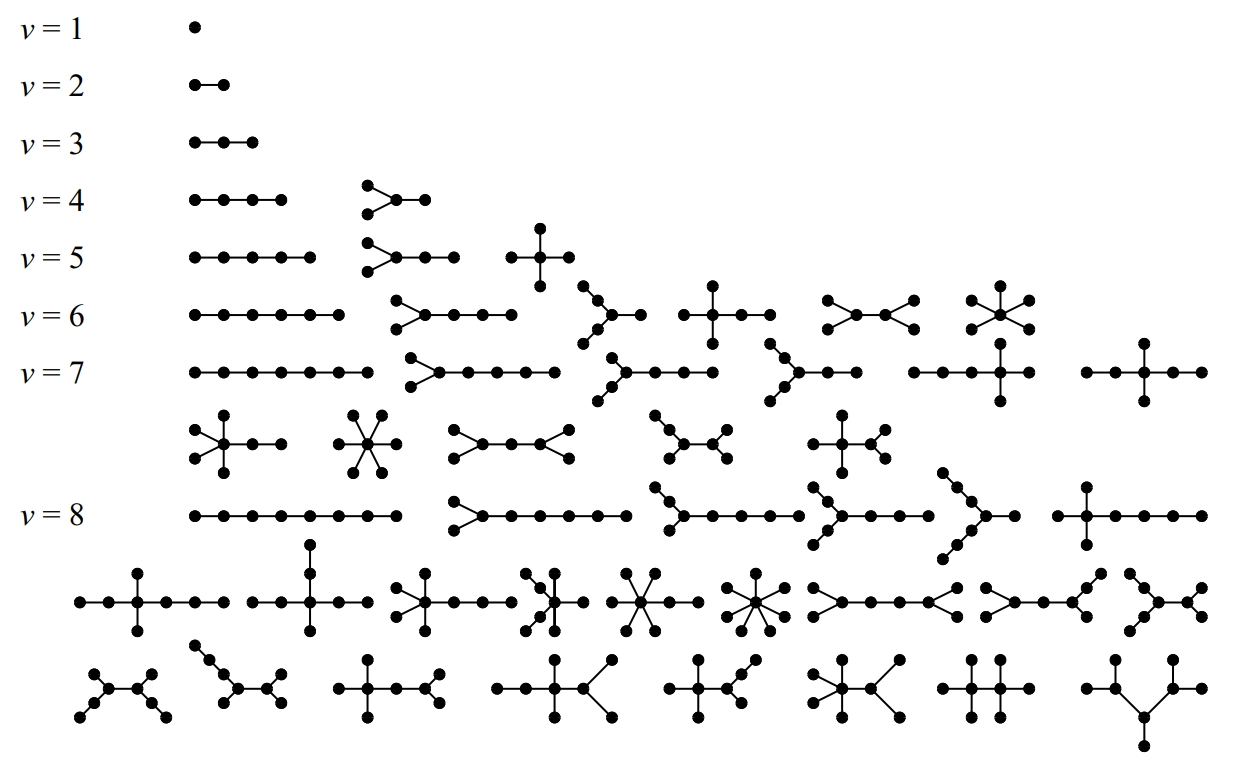
Tots els arbres amb vuit vèrtexs com a màxim
© fototeca.cat
Matemàtiques
Graf connex i acíclic (sense circuits).
Un arbre té només un vèrtex, anomenat arrel sense predecessor en el sentit de les fletxes, mentre que tot altre vèrtex té, cada un, un únic predecessor Tots els vèrtexs tenen un nombre variable de successors, que ordinariàment hom suposa ordenats per exemple, d’esquerra a dreta i de vegades són anomenats branques En la representació habitual d’un arbre l’arrel se situa al capdamunt i els arcs se suposen recorreguts en sentit descendent Els arbres han passat d’ésser un cas particular de graf a rebre un tractament matemàtic específic Són particularment útils en la modelització de processos en…
àlgebra

Triàngle numèric, més tard conegut com a triangle de Pascal, d’un manuscrit xinès del 1303
© Fototeca.cat
Matemàtiques
Branca de les matemàtiques que estudia les estructures algèbriques dels conjunts.
Hom l’aplica, per tant, en les situacions on hi ha un conjunt ben definit i una noció clara d’operació entre els seus elements operació interna o entre aquests i els elements d’altres conjunts operació externa L’àlgebra ha evolucionat des de l’interès inicial per a resoldre problemes fonamentalment pràctics fins al desenvolupament del mètode abstracte Dues inclinacions diferents han desembocat en l’àlgebra moderna D’una banda, l’ àlgebra clàssica , simple instrument per a fer càlculs i resoldre equacions que usava només els conceptes immediats que hom reconeixia al problema les quantitats…
el·lipsoide
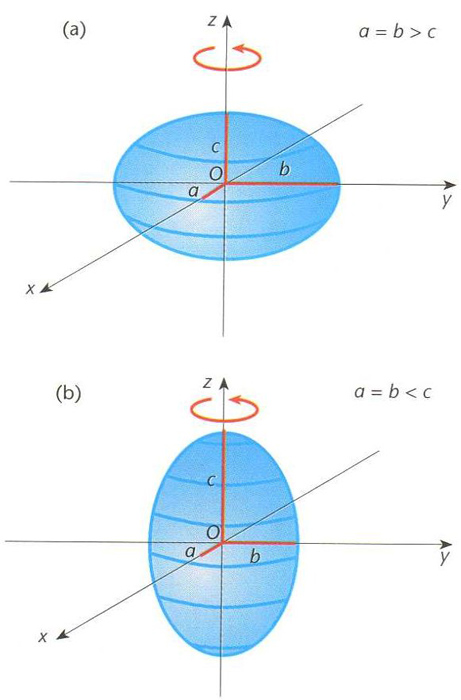
El·lipsoide aplatat (a) i allargat (b) obtinguts per rotació d’una el·lipse, prenent com a eix de la rotació el que conté, en el primer cas, el semieix menor d’aquesta el·lipse i, en el segon, el semieix major
© Fototeca.cat
Matemàtiques
Superfície de segon grau o quàdrica amb centre l’equació de la qual és (
x 2
/a 2
)+(
y 2
/b 2
)+(
z 2
/c 2
)=1 si els eixos de coordenades són els propis de la quàdrica.
Una ellipse que giri al voltant del seu eix menor determina un ellipsoide aplatat , anomenat també esferoide oblat i una ellipse que giri al voltant del seu eix major determina un ellipsoide allargat , anomenat també esferoide prolat Quan a=b=c=r l’ellipsoide esdevé una esfera de radi r
lògica algèbrica
Matemàtiques
Estudi algèbric de la lògica com a llenguatge (metallenguatge).
La lògica algèbrica tracta, doncs, les estructures que presenten les diferents lògiques i d’aquesta manera arriba a trobar estructures algèbriques —poc usuals en l’àmbit de l’àlgebra clàssica— com són, entre d’altres, les àlgebres de Hilbert, de Heyting, d’Abbott, de Boole, de Wajsberg, monàdiques, poliàdiques i cilíndriques
arrel
Matemàtiques
Quantitat x que, presa com a factor un cert nombre de vegades n, dóna com a producte una quantitat determinada a.
Hom ho expressa amb on a és el subradicand, x l’arrel i n l’índex aquesta expressió equival a x n = a El signe √sembla provenir de la deformació de la r inicial del mot llatí radix , ‘arrel’ àlgebra Una arrel d’índex 2 és anomenada arrel quadrada hom acostuma a suprimir gràficament l’índex d’índex 3, arrel cúbica d’índex 4, arrel biquadrada Les arrels de qualsevol altre índex no reben cap nom específic L’existència d’una arrel enèsima d’índex n q de p, on q i p són nombres reals i positius, és demostrada pel fet que la funció y = x n , on x varia de 0 a + ∞, és contínua i, per tant, pot…
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…
Reial Acadèmia de Ciències i Arts de Barcelona

Emblema de la Reial Acadèmia de Ciències i Arts de Barcelona
© Fototeca.cat
Entitats culturals i cíviques
Matemàtiques
Astronomia
Física
Química
Geologia
Biologia
Tecnologia
Institució fundada l’any 1764 amb el nom de Conferència Fisicomatemàtica Experimental amb Francesc Subiràs com a president i Josep Anton Desvalls, marquès de Llupià, com a secretari, limitada inicialment a 16 membres.
Celebrà les primeres reunions a la rebotiga d’una farmàcia i més tard a unes golfes del carrer de la Boqueria, on fou installat un gabinet de màquines d’experimentació El desembre del 1765 es reorganitzà amb el nom de Reial Conferència Física , amb uns nous estatuts pels quals fou designat president el capità general de Catalunya, i amplià el seu abast al conreu de “totes les ciències naturals i l’avenç de les arts útils”, amb nou seccions àlgebra i geometria estàtica i hidroestàtica electricitat magnetisme i òptica pneumàtica i acústica història natural botànica química…
correspondència
Matemàtiques
Una correspondència entre dos conjunts A
i B
és definida com un subconjunt del producte cartesià A × B
.
És fàcil de relacionar aquesta definició amb la idea intuïtiva de correspondència per exemple, si A és el conjunt dels països, i B el dels idiomes, la correspondència tal idioma es parla a tal país determina exactament un subconjunt de A × B el de les parelles a, b tals, que en el país a es parla l’idioma b En una correspondència el conjunt d’elements de A que apareixen com a primers elements de parelles de la correspondència és anomenat domini , i el conjunt d’elements de B que apareixen com a segons elements en les parelles de la correspondència, imatge Si cada element del domini només…
axioma
Filosofia
Matemàtiques
Proposició que hom admet sense demostració com a punt de partença d’una teoria o ciència.
Per a Aristòtil i fins a l’època moderna, els axiomes eren els principis evidents i irreductibles que constituïen els fonaments d’una ciència Actualment, sota la influència de la matemàtica moderna, els axiomes són els enunciats primitius anomenats també, a vegades, postulats acceptats com a vàlids sense provar-ne la veritat, dels quals deriven d’altres proposicions que s’organitzen en un sistema
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina