Resultats de la cerca
Es mostren 13 resultats
connex | connexa
Matemàtiques
Dit de l’espai topològic les úniques parts obertes i alhora tancades del qual són el conjunt buit i el propi conjunt.
espai connex
Matemàtiques
Espai topològic que no es pot expressar com a reunió disjunta de dos subespais oberts no buits.
Tot espai topològic arc-connex , és a dir, que donats dos punts de l’espai hi ha un arc de corba que els uneix contingut dins l’espai, és connex
espai localment connex
Matemàtiques
Espai topològic (X,OOO) quan en un punt x,y ∈ X si, i solament si, tot entorn d’x conté un entorn connex que conté x
.
espai arco-connex
Matemàtiques
Espai topològic OOOX,OOO si, i solament si, dos punts qualssevol x,y ∈ X poden ésser units per un arc; és a dir, per la imatge contínua d’un segment.
teorema de Bonnet
Matemàtiques
Teorema segons el qual els coeficients de les formes fonamentals d’una superfície determinen localment la parametrització de la superfície, llevat de composició amb transformacions ortogonals pròpies i translacions.
Concretament, si E , F , G , e , f , g són funcions diferenciables definides en un obert V ⊂ ℝ 2 , amb E > 0, G > 0 i EG – F 2 > 0 tals que satisfan les equacions de compatibilitat de Gauss i de Mainardi-Codazzi, aleshores per a cada q ∈ V existeix un entorn U ⊂ V de q i un difeomorfisme x U → x U ⊂ ℝ 3 tal que la superfície regular x U ⊂ ℝ 3 té E , F , G , e , f , g per coeficients en les seves formes fonamentals Amés, si U és connex i x’ U → x’ U ⊂ ℝ 3 és un altre difeomorfisme que satisfà les mateixes condicions, aleshores existeix una translació T i una…
component connexa
Matemàtiques
En un espai topològic, subespai connex
.
Sigui un punt x d’un espai topològic , és la unió de tots els subconjunts connexos de X que contenen x Les components connexes són sempre tancades i, si són diferents són disjuntives
arbre
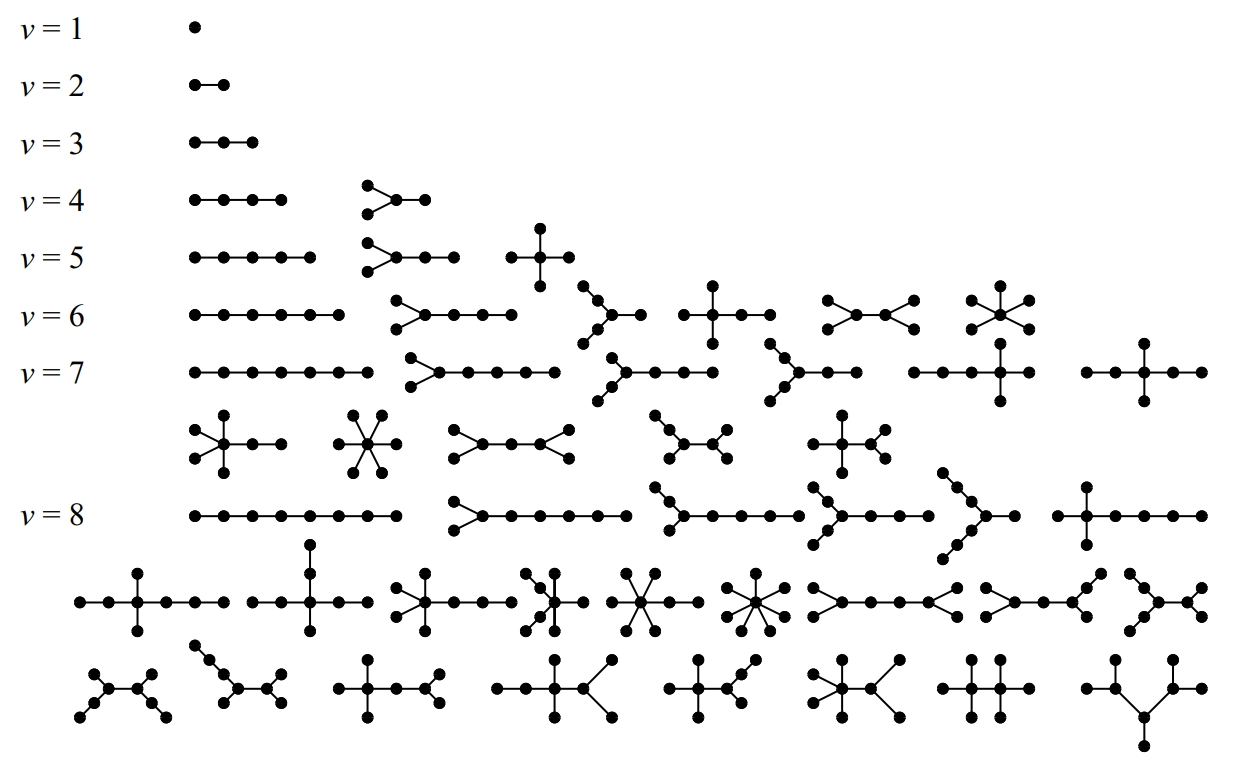
Tots els arbres amb vuit vèrtexs com a màxim
© fototeca.cat
Matemàtiques
Graf connex i acíclic (sense circuits).
Un arbre té només un vèrtex, anomenat arrel sense predecessor en el sentit de les fletxes, mentre que tot altre vèrtex té, cada un, un únic predecessor Tots els vèrtexs tenen un nombre variable de successors, que ordinariàment hom suposa ordenats per exemple, d’esquerra a dreta i de vegades són anomenats branques En la representació habitual d’un arbre l’arrel se situa al capdamunt i els arcs se suposen recorreguts en sentit descendent Els arbres han passat d’ésser un cas particular de graf a rebre un tractament matemàtic específic Són particularment útils en la modelització de processos en…
arbre arrelat
Matemàtiques
Graf orientat connex, sense cicles i amb un vèrtex distingit anomenat arrel, de tal manera que hi ha un únic camí de l’arrel fins a cada vèrtex.
En la representació habitual d’un arbre arrelat, l’arrel se situa al capdamunt i els arcs se suposen recorreguts en sentit descendent