Resultats de la cerca
Es mostren 6 resultats
convex | convexa
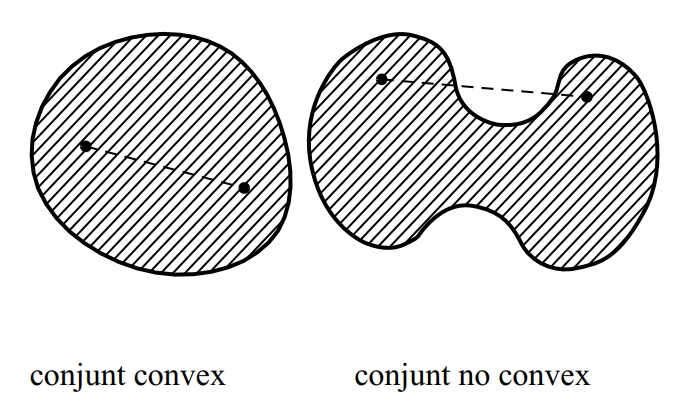
convex
Matemàtiques
Dit de la figura tal que el segment que uneix un parell qualsevol dels seus punts està totalment contingut en el seu interior.
angle convex
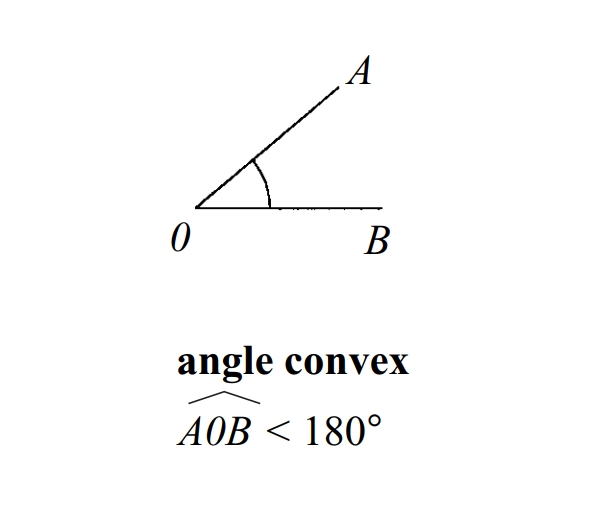
angle convex
Matemàtiques
Angle que és menor que la suma de dos angles rectes de tal manera que les prolongacions dels costats li són exteriors.
políedre
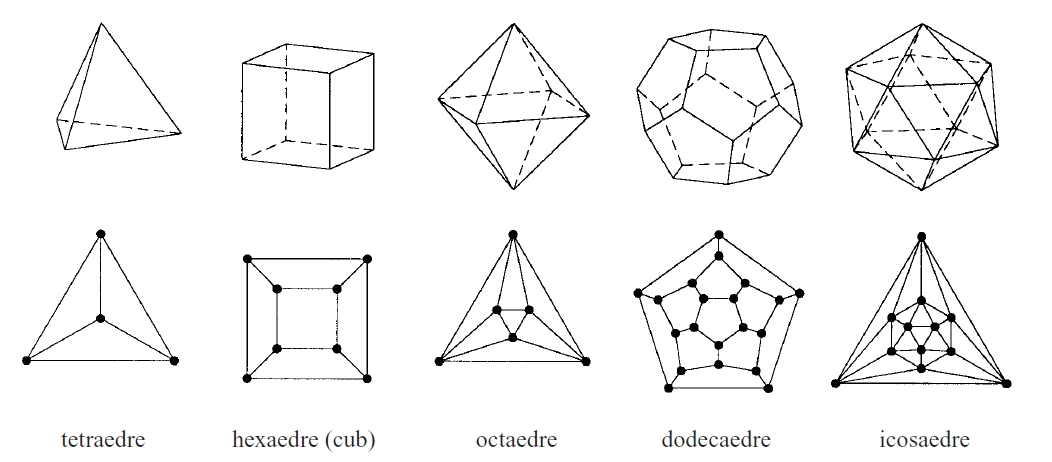
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
Matemàtiques
Sòlid limitat per quatre o més polígons anomenats cares.
Les interseccions de les cares constitueixen les arestes , i les interseccions de les arestes, els vèrtexs Un políedre és convex si qualsevol secció plana del políedre és un polígon convex Un políedre és còncau si no és convex Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars el tetràedre regular , l’ hexàedre regular o cub, l’…
polígon
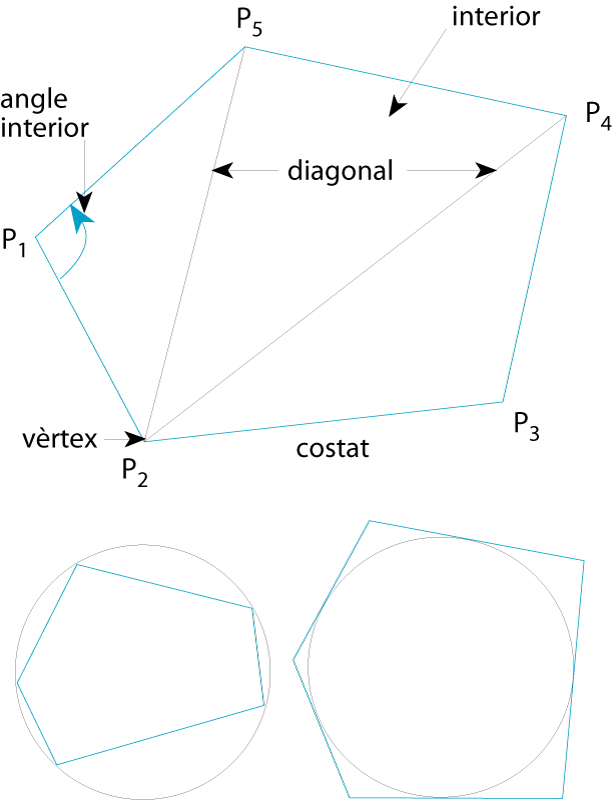
Elements d’un polígon (dalt); polígon inscrit en un cercle (baix esquerre); polígon circumscrit a un cercle (baix dreta)
© Fototeca.cat
Matemàtiques
Figura plana i tancada formada per segments rectes.
P 1 P 2 , P 2 P 3 , P n - 1 P n , i P n P 1 , són anomenats costats del polígon, essent els punts P 1 , P 2 , , P n , amb n ≥3, els anomenats vèrtexs del polígon Una diagonal del polígon és el segment recte que uneix dos vèrtexs no correlatius La porció de pla que és envoltada pels costats constitueix l' interior del polígon Els angles determinats per cada parell de costats adjacents, i que són a l’interior, són dits angles interiors del polígon Un polígon és convex si cada angle interior és menor o igual a 180° Un polígon és còncau si no és convex, és a dir, si…
políedre estelat
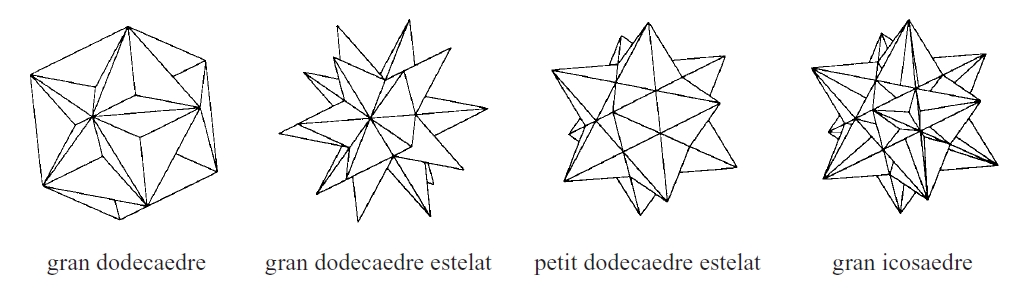
Els quatre políedres estelats regulars
Matemàtiques
Políedre que s’obté de col·locar piràmides sobre les cares d’un políedre convex o de prolongar-ne les cares.
teorema de Ptolemeu
Matemàtiques
Teorema segons el qual la condició necessària i suficient perquè un quadrilàter convex sigui inscriptible en un cercle és que el producte de les diagonals sigui igual a la suma dels productes dels costats oposats, és a dir, si A, B, C i D són els vèrtexs del quadrilàter, la condició es AC · BD = AB · CD + AD · BC.