Resultats de la cerca
Es mostren 10 resultats
René Thom
Matemàtiques
Matemàtic francès.
Treballà en el camp de la topologia diferencial rebé la medalla Fields el 1958, disciplina en la qual generà el concepte de cobordisme Fou especialment conegut per haver desenvolupat la teoria de les catàstrofes És autor, entre d’altres, de Stabilité structurelle et morphogenèse 1972
Shigefumi Mori

Shigefumi Mori
© International Mathematical Union
Matemàtiques
Matemàtic japonès.
Graduat a la Universitat de Kyoto l’any 1975, es doctorà el 1978 amb una tesi sobre l’endomorfisme dels anells en variants abelianes Posteriorment fou professor assistent en aquesta universitat fins el 1980, que passà a la Universitat de Nagoya, on fou nomenat professor titular el 1988 L’any 1990 retornà a la Universitat de Kyoto, on ocupa una càtedra Des del 1977 ha estat professor visitant en diverses universitats dels EUA El seu interès se centra en la geometria algèbrica, i ha desenvolupat tècniques per tal de resoldre el problema de la classificació completa de les varietats…
lògica difusa
Matemàtiques
Tipus de lògica en què els valors de certesa i falsedat s’expressen en graus, i no de manera absoluta.
La lògica clàssica s’interpreta en la teoria dels conjunts cert indica la pertinença a un determinat conjunt fals, la no-pertinença La lògica difusa usa la teoria dels conjunt difusos, on la pertinença o no-pertinença és una qüestió de grau Per exemple, la pertinença al conjunt dels alts pot quedar molt clara en alguns casos, però més obscura o difusa en d’altres La lògica difusa s’usa bastant en l’anàlisi del llenguatge natural, en sistemes experts, i en general en tot tipus d’heurísticEls darrers temps s’han desenvolupat dispositius electrònics i productes comercials basats en…
Abraham De Moivre
Matemàtiques
Matemàtic anglès d’origen francès.
Estudià a les universitats de Sedan, Saumur i París Després de la revocació de l’edicte de Nantes es traslladà a Anglaterra per tal de fugir de la persecució desencadenada a França contra els hugonots Ja a Anglaterra, l’astrònom EHalley presentà el seu treball “Specimen” 1967 a la Royal Society, de la qual fou elegit membre dos anys més tard La majoria dels seus treballs foren publicats en les Philosophical Transactions Arran de la polèmica entre Newton i Leibniz sobre la invenció del càlcul, formà part de la comissió que estudià el problema El seu primer estudi sobre probabilitat, De…
Yves Meyer
Matemàtiques
Matemàtic francès.
Graduat en matemàtiques per l’Escola Normal Superior ENS de París 1957, obtingué el doctorat per la Universitat d’Estrasburg el 1966 Ha desenvolupat la seva trajectòria docent i de recerca successivament a l’escola militar Prytanée 1960-63, la Universitat d’Estrasburg 1963-66, la Universitat de París-Sud 1966-80, l’École Polytechnique 1980-86, la Universitat de París-Dauphiné 1985-95 i al centre de matemàtiques CMLA de l’ENS fins a la jubilació 2008, d’on fou nomenat professor emèrit Ha fet aportacions a la teoria dels nombres i, especialment, a l’anàlisi harmònica, camp en el…
Terence Tao
Matemàtiques
Matemàtic australià.
Fill d’emigrants de Hong Kong Graduat 1991 i màster 1992 per la Universitat de Flinders, el 1996 es doctorà per la Universitat de Princeton Professor de la Universitat de Califòrnia Los Angeles UCLA des del 1996, els seus camps de recerca inclouen, entre d’altres, l’anàlisi harmònica, les equacions diferencials parcials, la combinatòria algèbrica, la combinatòria aritmètica, la combinatòria geomètrica, la teoria de probabilitats, la compressió de dades i la teoria dels nombres En aquest camp, el 2004 enuncià, conjuntament amb el matemàtic britànic Ben J Green, el teorema de Green-Tao ,…
arrel
Matemàtiques
Quantitat x que, presa com a factor un cert nombre de vegades n, dóna com a producte una quantitat determinada a.
Hom ho expressa amb on a és el subradicand, x l’arrel i n l’índex aquesta expressió equival a x n = a El signe √sembla provenir de la deformació de la r inicial del mot llatí radix , ‘arrel’ àlgebra Una arrel d’índex 2 és anomenada arrel quadrada hom acostuma a suprimir gràficament l’índex d’índex 3, arrel cúbica d’índex 4, arrel biquadrada Les arrels de qualsevol altre índex no reben cap nom específic L’existència d’una arrel enèsima d’índex n q de p, on q i p són nombres reals i positius, és demostrada pel fet que la funció y = x n , on x varia de 0 a + ∞, és contínua i, per tant, pot…
estadística econòmica i social
Matemàtiques
Branca de l’estadística aplicada que utilitza els mètodes quantitatius en l’estudi numèric dels fenòmens col·lectius de caràcter econòmic i social.
Té dues branques, l' estadística descriptiva , desenvolupada ja als s XVIII i XIX, i l' estadística teòrica , que s’ha desenvolupat principalment al s XX Als Països Catalans, la primera anàlisi estadística és l' Estadística de Barcelona en 1849 , de Laureà Figuerola es refereixen també a la ciutat les publicacions a la Teoría general de la urbanización 1867, d’Ildefons Cerdà, i els treballs de Gumersind Colomer i Codina 1883 i de Pere Garcia i Fària 1893 A Mallorca és important el treball de Casimir Urech i Cifre Estudios sobre la riqueza territorial de las islas Baleares 1869 Un…
teoria de les catàstrofes
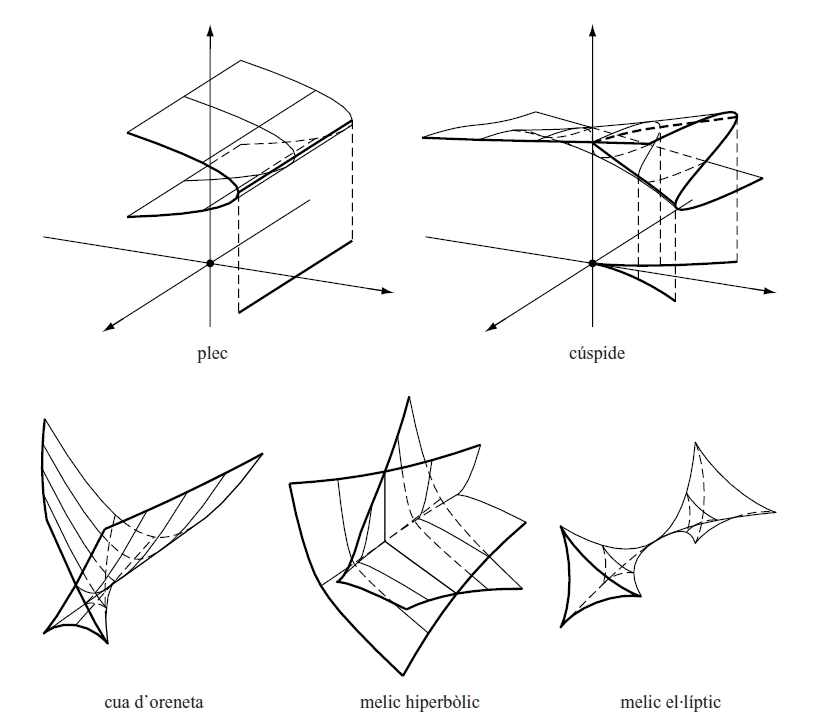
teoria de catàstrofes Les cinc catàstrofes elementals de codimensió menor que quatre
Física
Matemàtiques
Corpus teòric desenvolupat pel matemàtic francès René Thom d’ençà del 1972, i originat en l’intent de modelitzar els canvis discontinus que hom observa en la natura.
En molts sistemes, una petita variació quantitativa de les condicions inicials dóna lloc a una enorme diferència qualitativa en el comportament a llarg termini del sistema situació anomenada bifurcació de comportament Això és important per a l’estudi dels fenòmens d’estabilitat estructural, on cal que el sistema sigui insensible a petites pertorbacions En la teoria de les catàstrofes, aquest requeriment implica que el sistema dinàmic que modelitza el fenomen natural pugui ésser descrit localment per mitjà d’una de les set formes normals conegudes com a catàstrofes elementals , tot i que…
topologia

Topologia Les figures unides amb fletxes són topològicament iguals, perquè és possilbe passar de l’una a l’altra per mitjà d’una transformació contínua
© Fototeca.cat
Matemàtiques
Part de la matemàtica que estudia aquelles propietats dels conjunts de punts de la recta, del pla, de l’espai o d’espais de dimensions superiors que no són alterades per les transformacions contínues.
Es tracta de propietats geomètriques que no depenen de cap magnitud, sinó únicament de la posició relativa dels punts Per exemple, el fet que dos punts puguin unir-se o no per un camí, o que el nombre de cares menys el d’arestes més el de vèrtexs d’un políedre esfèric sigui sempre dos teorema d’Euler Aquí hom entén per transformació contínua aquella que admet una inversa i que tant ella com la inversa són contínues L’íntima connexió que hi ha entre el concepte de continuïtat d’una funció en un punt i el d’entorn d’un punt permet de transportar l’estudi de propietats topològiques a aquells…