Resultats de la cerca
Es mostren 6 resultats
diàmetres conjugats
Matemàtiques
En una cònica, un diàmetre qualsevol i el definit per un sistema de cordes paral·lel al primer.
fletxa
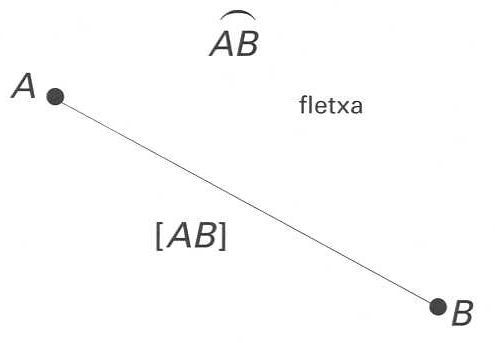
Fletxa d’un arc de corba AB
©
Matemàtiques
En un arc de corba AB, segment que uneix el centre de l’ar c AB amb el centre de la corda [AB].
Si AB és un arc d’una circumferència, la fletxa és situada sobre el diàmetre perpendicular a la corda AB , i la seva longitud és l = r 1—cosα/2, on r és el radi de la circumferència i α l’angle determinat pels diàmetres subtendits pels extrems de l’arc
cònica
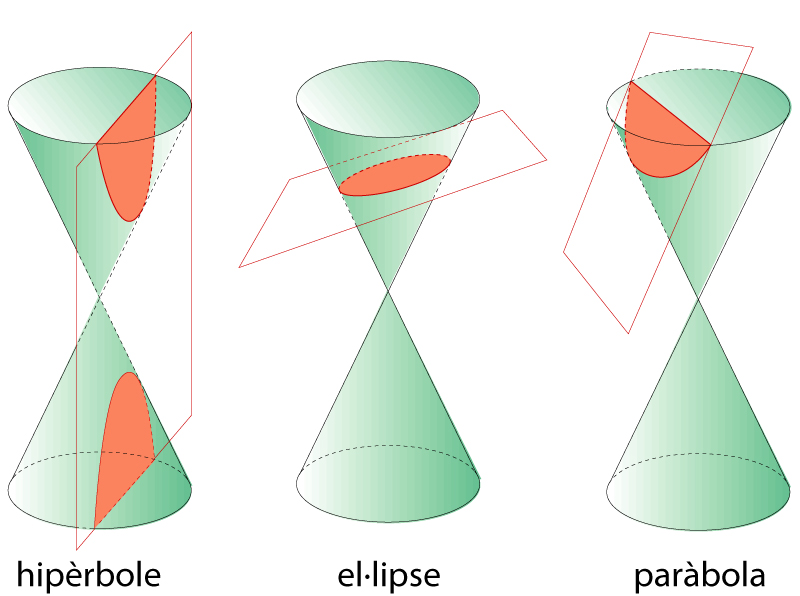
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…
integral múltiple
Matemàtiques
Integral definida sobre un domini D de ℝn.
Donat un domini D de ℝ n , i una partició en dominis elementals D i d’àrees a i i diàmetres d i , i donada una funció real definida sobre D , fD ⊂ ℝ n → ℝ, límit I quan els d i tendeixen a 0, de les sumes de Riemann on A i ∈ D i Hom diu que I és la integral de f en D i és notada per ʃ ʃ n ʃ D ʃ x 1 , x n d x 1 dx n Els casos particulars n =2 i n =3 constitueixen la integral doble i la integral triple, respectivament Les integrals múltiples poden ésser calculades per integració unidimensional reiterada
esfera
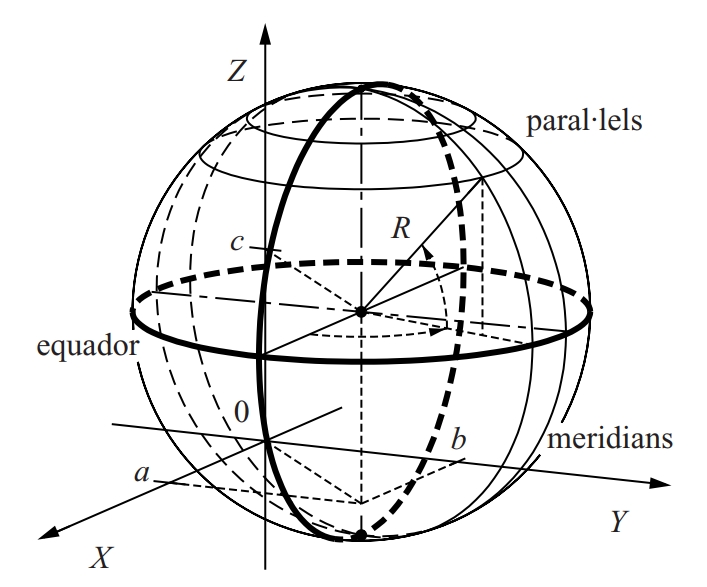
Esfera de centre (a, b, c) i radi R
Matemàtiques
Figura espacial generada per la rotació d’un cercle al voltant d’un dels seus diàmetres.
Es tracta d’una quàdrica amb equació cartesiana x – a 2 + y – b 2 + z – c 2 = R 2 si el centre és el punt a , b , c i el radi és R El seu volum val i la seva superfície S = 4 π R 2
conjugat | conjugada
Matemàtiques
Dit de dues magnituds (punts, corbes, quantitats, estructures, operadors, etc) enllaçades per alguna llei o relació determinada (diàmetres conjugats d’una el·lipse, nombres complexos conjugats).