Resultats de la cerca
Es mostren 10 resultats
antiparal·lel | antiparal·lela
recta isòtropa
Matemàtiques
Recta del pla o de l’espai complex que satisfà la condició d’ésser perpendicular a ella mateixa.
Les rectes isòtropes defineixen les anomenades direccions isòtropes
paral·lelisme
Matemàtiques
Qualitat de paral·lel.
La relació de parallelisme, definida tant en el conjunt de rectes com en el conjunt de plans, és una relació d’equivalència El conjunt quocient, en el cas de les rectes, és el conjunt de direccions
mosaic
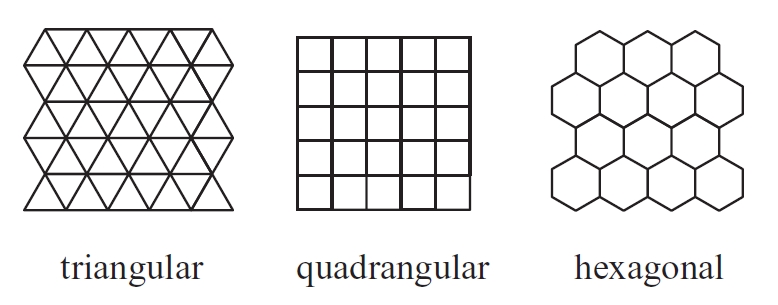
mosaics
© Fototeca.cat
Matemàtiques
Recobriment del pla per repetició d’un mòdul fix segons dues direccions.
Els mosaics regulars s’obtenen per repetició d’un polígon regular Els mosaics semiregulars es generen en combinar dos tipus de polígons regulars de dimensions convenients per al seu acoblament Únicament hi ha tres tipus de mosaics regulars i vuit de semiregulars Els únics mosaics regulars que es poden construir al pla són el triangular, el quadrangular i l’hexagonal
producte vectorial de dos vectors
Matemàtiques
Operació definida entre dos vectors.
Donats dos vectors, a i b , vector a ∧ b el mòdul del qual és | a ∧ b | = | a | | b | sin a , b , on sin a , b és el sinus de l’angle que determinen les direccions de a b , i la direcció del qual és perpendicular al pla determinat per a i b , i el sentit del qual és tal que el tríedre a , b , a ∧ b sigui dextrogir és a dir, que el sentit de a ∧ b és igual al sentit d’avanç d’un llevataps que, aplicat en el punt de concurrència de a i b , anés del primer cap al segon
perspectiva cavallera
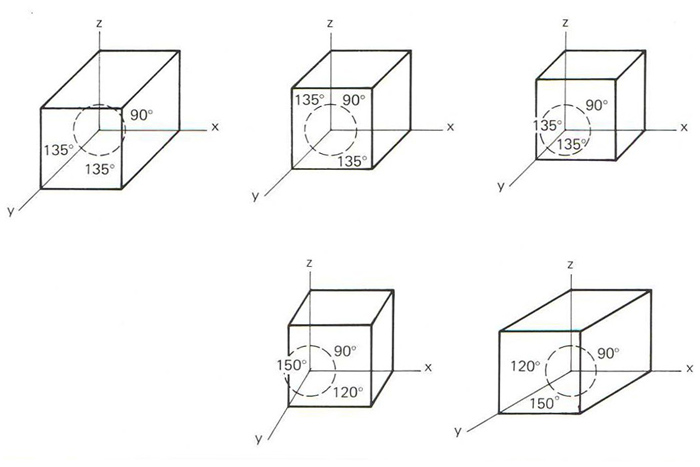
Representació d’un cub amb diferents reduccions i angles
© fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Projecció cilíndrica obliqua d’un cos sobre el pla de projecció (pla del quadre).
En aquest cas el pla del quadre és el mateix pla coordenat OXZ, i per això les rectes paralleles als eixos OZ i OX es projecten en llur veritable magnitud L’eix Y és projectat en el quadre amb una direcció dependent de la que tinguin les projectants, i sofreix, per tant, la reducció Per a les representacions en aquest sistema, caldrà conèixer la reducció de l’eix Y i el valor de l’angle XOY o YOZ, que oscillarà entre 0º i 360º aquesta relació serà constant per a totes les línies paralleles a l’eix Y L’angle que forma l’eix Y amb l’eix X podria ésser elegit indistintament, però evitant els…
perspectiva axonomètrica
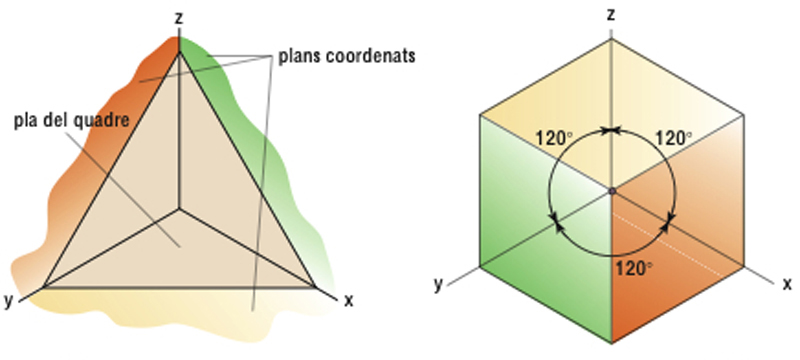
Elements de la perspectiva axonomètrica (isomètrica) i representació d’un cub
© Fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Sistema de representació que consisteix a referir els objectes que han d’ésser representats —mitjançant projeccions ortogonals— als plans d’un tríedre trirectangle ( plans coordenats
) i projectar-los, després, sobre un quart pla ( pla del quadre
) oblic als anteriors ( axonometria
).
El seu traçat es redueix a dibuixar les direccions dels cossos parallelament a la projecció dels eixos coordenats, relacionant amb ells les mesures d’alçada, amplada i profunditat Definit el pla del quadre, les projeccions de les arestes del tríedre sobre el pla no són donades en llurs veritables magnituds, sinó que tindran una magnitud menor Això equival a dir que totes les línies de l’espai paralleles a un pla del tríedre es veuran reduïdes en la mateixa proporció La relació entre la magnitud sobre el pla del quadre d’una de les arestes i la seva veritable magnitud és denominada coeficient…
sinclàstic | sinclàstica
Matemàtiques
Dit de les superfícies corbades en el mateix sentit en totes les direccions a partir d’un punt.
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un espai vectorial de dimensió…
anàlisi matemàtica

anàlisi matemàtica Portada dels Philosophiae Naturalis Principia Mathematica de Newton (1687)
© Fototeca.cat
Matemàtiques
Part de les matemàtiques bastida sobre els conceptes bàsics de funció, límit, continuïtat, derivada i integral.
És el desenvolupament modern del càlcul infinitesimal, elaborat durant els segles XVII i XVIII, que tenia com a principals problemes el de les quadratures determinació de la longitud d’una corba i de les àrees i volums de figures i el de la tangència traçat de tangents a corbes i superfícies Els coneixements que s’anaren acumulant sobre aquests temes formaren els càlculs integral i diferencial, cor d’aquesta disciplina matemàtica L’anàlisi matemàtica presenta els trets distintius de l’abstracció i generalitat dels seus mètodes, característics del rigor del raonament lògic És el resultat d’una…