Resultats de la cerca
Es mostren 67 resultats
espai normal
Matemàtiques
Espai topològic en el qual, donats dos espais tancats disjunts, n’hi ha dos d’oberts també disjunts que els contenen.
Un teorema d’Urysohn afirma que en un espai normal, donats dos espais tancats disjunts, hi ha una funció real contínua que pren el valor zero en l’un i el valor u en l’altre
bisector
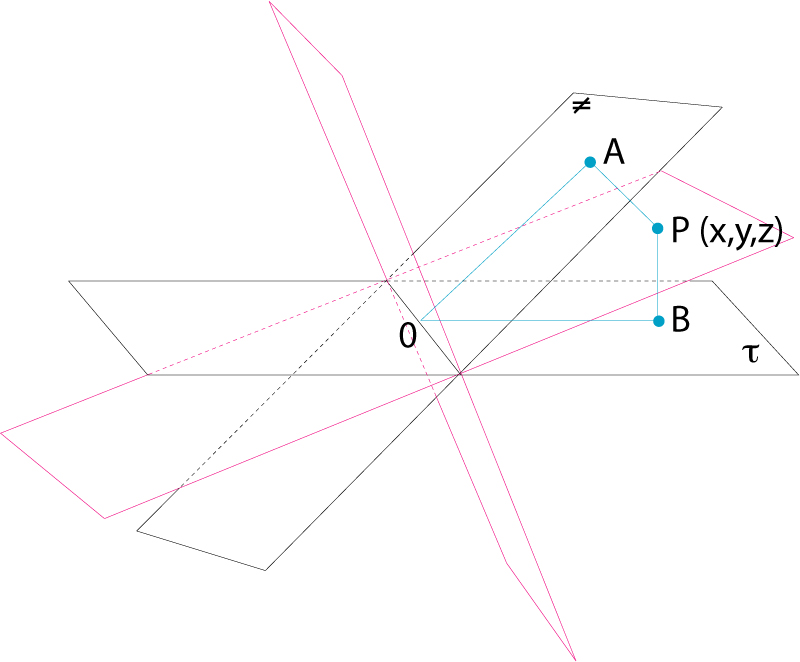
Plans bisectors dels quatre díedres formats per dos plans donats que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels dos plans costats d’un angle díedre, el qual, per tant, és dividit en dos díedres iguals.
Dos plans no parallels determinen quatre angles díedres, per als quals hom distingeix dos plans bisectors Per a cada díedre, un dels plans bisectors serà interior, i l’altre, exterior Si les equacions cartesianes de dos plans són A 1 x + B 1 y + C 1 z + D 1 = 0 i A 2 x + B 2 y + C 2 z + D 2 = 0, en una referència cartesiana normal, l’equació dels dos plans bisectors dels díedres que aquells determinen és
interpolació
Matemàtiques
Procediment que, donats els n valors y 1, y 2, ..., yi, ..., yn d’una funció y = g(x) en els punts x 1, x 2..., xi, ..., xn, permet de calcular, aproximadament, els valors de g(x) en punts intermedis als donats.
Més exactament, la interpolació consisteix a trobar una altra funció y = f x , d’un tipus escollit, que passi pels punts x i , y i Una primera aproximació és constituïda per la interpolació lineal , que consisteix a imposar que, entre cada dos punts consecutius dels donats, f x sigui un segment de recta En la interpolació de Lagrange , f x és un polinomi de grau n- 1 donat per la fórmula Si els punts x i constitueixen una progressió aritmètica, és emprada la interpolació de Newton càlcul de diferències diferència
polinomis de Laguerre
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
Satisfan la fórmula de recurrència n +1 L n ₊₁ x + x-2n-1 L n x + n L n ₋₁ x = 0, i són solucions de l' equació diferencial de Laguerre, xy n + 1- x y’ + ny = 0 Els primers polinomis són L₀ x = 1, L₁ x = 1- x, L₂ x = 1-2 x + x 2 /2 Satisfan la següent ortogonalitat on és el símbol de Kronecker
polinomis d’Hermite
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
Satisfan la fórmula de recurrència H n + 1 x - 2 xH n x + 2 nH n - 1 x = 0, i són solucions de l' equació diferencial d’Hermite, y n - 2 xy + 2 ny = 0 Els primers polinomis són H 0 x = 1, H 1 x = 2 x , H 2 x = 4 x 2 -2, etc Satisfan la següent ortogonalitat on δ p q és el símbol de Kronecker
polinomis de Legendre
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
.
Satisfan la fórmula de recurrència n +1 P n + 1 x - 2n+1 P n x + nP n - 1 x =0, i són solucions de l' equació diferencial de Legendre , 1- x 2 y´´ - 2 xy ´ + n n +1 y = 0 Els primers polinomis són P 0 x = 1, P 1 x = x , P 2 x = 3 x 2 -1 /2 Satisfan la següent ortogonalitat on és el símbol de Kronecker
distància euclidiana
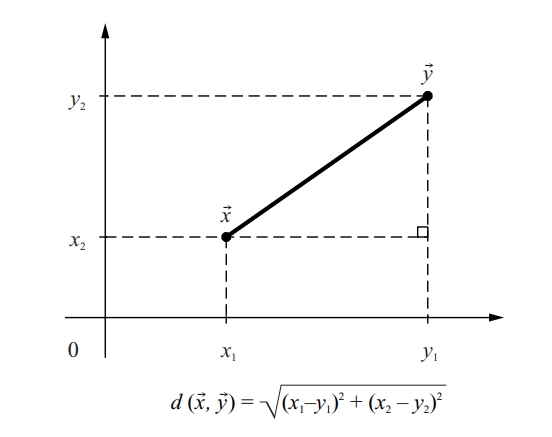
distància euclidiana
Matemàtiques
Distància definida a ℝ n.
Donats dos punts x = x 1 , , x n i y = y 1 , , y n de ℝ n , aquesta distància és definida per
espai connex
Matemàtiques
Espai topològic que no es pot expressar com a reunió disjunta de dos subespais oberts no buits.
Tot espai topològic arc-connex , és a dir, que donats dos punts de l’espai hi ha un arc de corba que els uneix contingut dins l’espai, és connex
raó simple
Matemàtiques
Donats tres punts alineats A, B i C, relació
.
La raó simple és un invariant en una projecció
semireticle
Matemàtiques
Conjunt ordenat en el qual, donats dos elements, sempre existeix el suprem (element que és el més petit major que els dos donats).
També és possible la definició dual, que exigeix l’existència d’un ínfim
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Pàgina següent
- Última pàgina