Resultats de la cerca
Es mostren 9 resultats
representació
Matemàtiques
Donat un grup, grup (de permutacions, matrius o transformacions) que li és isomorf.
Quan hom tracta amb grups abstractes, sovint és interessant d’emprar una representació del grup , per tal d’operar millor amb ell Tot grup finit pot ésser representat per un grup de permutacions o de matrius
trisecció d’un angle

Trisecció d’un angle, mitjançant la "destral índia"
Matemàtiques
Divisió d’un angle en tres angles iguals.
La trisecció d’un angle constituí un dels problemes clàssics, i hom demostrà que és insoluble gràficament mitjançant el regle i el compàs per a la solució cal emprar corbes d’ordre superior al segon, com la concoide de Nicomedes
Georg von Purbach
Astronomia
Matemàtiques
Matemàtic i astrònom austríac.
Professor a diverses ciutats d’Itàlia i a Viena, on tingué com a deixeble Johann Müller Inicià la traducció al llatí de l' Almagest de Ptolemeu, que després completà el seu deixeble Confeccionà la taula dels sinus i fou un dels primers a emprar-los en trigonometria
prova de khi quadrat
Matemàtiques
Prova de significació emprada per a sèries grans d’observacions, que mesura l’acostament entre la distribució de les dites observacions i una distribució de freqüències teòricament establerta, dita de χ 2
.
Si F i designa les freqüències experimentals i P i les freqüències esperades teòricament, hom calcula la fidelitat de la distribució experimental envers la de χ 2 per mitjà de la fórmula χ 2 =0 en el cas de coincidència entre totes dues distribucions Hom sol emprar aquesta prova per al contrast d’hipòtesis, amb uns marges de fiabilitat del 95 o del 99%, i és aplicable a situacions molt diverses
càlcul de diferències
Matemàtiques
Estudi de les propietats d’una funció de la qual hom només coneix un conjunt finit de valors f(x0), f(x1), ..., f(xn), que corresponen als arguments x0, x1, ..., xn, els quals, habitualment, són presos en progressió aritmètica xr=x0+rϖ.
Hom defineix l’ operador diferència Δ, mitjançant l’expressió Δf x = f x + ϖ - f x , i l’ operador incremental E , definit per E ϖ f x = f x + ϖ = f x + Δ f x , de manera que E = 1+Δ Les propietats d’aquests permeten d’assolir el resultat següent, dit teorema de Gregory f x + nϖ = E nϖ f x = 1+Δ n f x , on, en l’última expressió, hom pot emprar la fórmula del binomi de Newton Aquests operadors poden expressar les diferències dividides Hom pot obtenir una aproximació polinòmica a la funció f x amb la fórmula d’interpolació de Newton en la qual, si f x és n vegades…
arrel
Matemàtiques
Quantitat x que, presa com a factor un cert nombre de vegades n, dóna com a producte una quantitat determinada a.
Hom ho expressa amb on a és el subradicand, x l’arrel i n l’índex aquesta expressió equival a x n = a El signe √sembla provenir de la deformació de la r inicial del mot llatí radix , ‘arrel’ àlgebra Una arrel d’índex 2 és anomenada arrel quadrada hom acostuma a suprimir gràficament l’índex d’índex 3, arrel cúbica d’índex 4, arrel biquadrada Les arrels de qualsevol altre índex no reben cap nom específic L’existència d’una arrel enèsima d’índex n q de p, on q i p són nombres reals i positius, és demostrada pel fet que la funció y = x n , on x varia de 0 a + ∞, és contínua i, per tant, pot…
integral
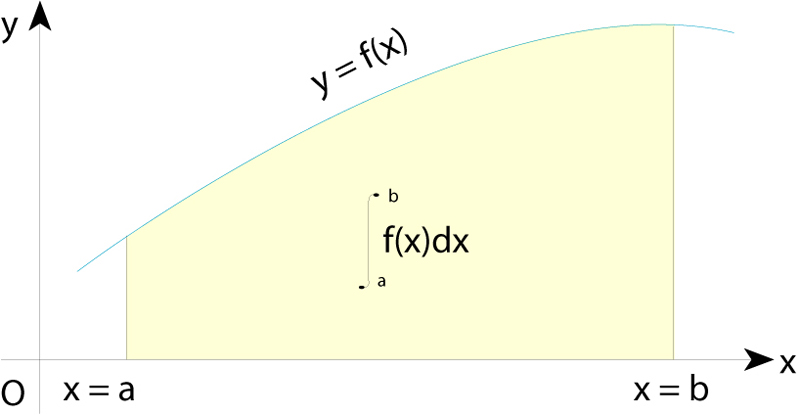
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b , hom determina en cada subinterval x i - 1 , x i els termes M i…
investigació operativa
Matemàtiques
Branca de les matemàtiques molt lligada a l’estadística i a l’anàlisi dels processos d’optimització, consistent a aplicar tècniques matemàtiques i estadístiques a la solució de problemes governamentals, empresarials, industrials, educatius, etc.
Les tècniques de la investigació operativa són particularment útils en l’equilibrament d’objectius conflictius amb un gran nombre de línies d’acció alternatives, amb conflictes d’interessos i amb un gran nombre de variables complexes i interaccionants La investigació operativa s’utilitza per a conduir i coordinar les operacions o les activitats dins un sistema organitzat empresa, administració pública, etc, i els estudis que en són el resultat intenten proporcionar a l’executiu una base sòlida, científica i quantitativa per a la presa de decisions Es caracteritza també per l’aplicació del…
aritmètica
Matemàtiques
Estudi dels nombres naturals i de les operacions d’addició, subtracció, multiplicació, divisió entera, potenciació i extracció d’arrels enteres entre aquests nombres.
L’aritmètica ha nascut a totes les civilitzacions ensems amb el llenguatge per anomenar conjunts de persones o d’objectes i després per facilitar els intercanvis comercials Els egipcis s’havien ocupat d’alguns problemes aritmètics, i les obres que n'han estat conservades la més antiga de les quals és el papir Rhind ~s XVII aC contenen la resolució d’algunes qüestions numèriques sense dir en quines propietats recolza la resolució, ni menys encara justificar-les El nivell de llurs coneixements era, aproximadament, el de l’actual ensenyament primari, però eren enunciats amb un llenguatge més…