Resultats de la cerca
Es mostren 14 resultats
arrel enèsima
Matemàtiques
Donat un nombre real o complex, anomenat radicand, nombre real o complex que, elevat a n, dóna el radicand.
enèsim | enèsima
Matemàtiques
Dit d’una potència, arrel, ordre de derivació, etc, indeterminats.
enèsim | enèsima
Matemàtiques
Dit de cadascuna de les parts d’una quantitat dividida en un nombre indeterminat de parts iguals designat per la lletra n.
enèsim | enèsima
Matemàtiques
En una sèrie o successió indefinides, dit del terme que ocupa un lloc general indeterminat, designat per la lletra n.
teorema de la integral de Cauchy
Matemàtiques
Teorema relatiu a la integració en el camp complex que afirma que, per a tota funció f(z), de variable z complexa, holomorfa en un recinte simplement connex D, i per a qualsevol trajectòria tancada C continguda en D, es verifica: 72185.
Hom pot també enunciar aquest teorema dient que, en les condicions anteriors, la integral de f z entre dos punts de D és independent del camí d’integració elegit, sempre que aquest camí sigui contingut en D Aquest teorema és fonamental per a l’estudi de les funcions de variable complexa i dóna lloc a la teoria de la integració per residus integral Una aplicació immediata és la integral de Cauchy , mitjançant la qual hom pot expressar el valor d’una funció regular f z i de les seves derivades en un punt qualsevol a interior a un contorn al llarg de C , mitjançant les expressions on f a…
símbol
Matemàtiques
Lletra o signe gràfic de qualsevol mena utilitzat per a representar quantitats (nombres), relacions o operacions.
Cal distingir sempre el símbol del concepte Així, el nombre dos concepte pot ésser representat per símbols diferents 2, II, ╫, etc Principals símbols símbols emprats en teoria de conjunts ∈ pertany a ∉ no pertany a = igual a ≠ diferent ⊂ inclusió, és inclòs en ⊄ no és inclòs en ⋂ intersecció ⋃ reunió − diferència ∁ , − , ∽ complementari ∆ diferència simètrica → aplicació, funció ≃ coordinable, bijectiu x producte cartesià {} singletons claudàtors ∅ conjunt buit ℕ nombres naturals ℤ nombres enters ℚ nombres racionals ℝ nombres reals ℂ nombres complexos símbols emprats en lògica…
radical
Matemàtiques
Signe √ emprat per a indicar l’arrel enèsima d’una quantitat o expressió.
Hom hi indica, a més, l’índex n de l’arrel, llevat del cas en què n = 2, és a dir, en el cas de l’arrel quadrada arrel
càlcul de variacions
Matemàtiques
Estudi de la teoria dels extrems d’integrals definides tals, que llur integrant és una funció coneguda d’una o més variables independents, d’una o més variables dependents i de les seves derivades.
El problema consisteix a determinar les variables dependents, de manera que la integral sigui màxima o mínima En el cas més simple, la integral és de la forma on cal determinar la funció y x de manera que I sigui màxima o mínima També poden ésser considerades integrals de la forma on y 1 , , y n són funcions de x desconegudes o bé integrals múltiples tals com on z = z x,y és desconeguda com també poden ser-ho com integrals múltiples d’ordre superior o de diverses variables dependents L’integrant pot ésser també una funció en la qual intervinguin derivades parcials d’ordre superior En el…
mitjana
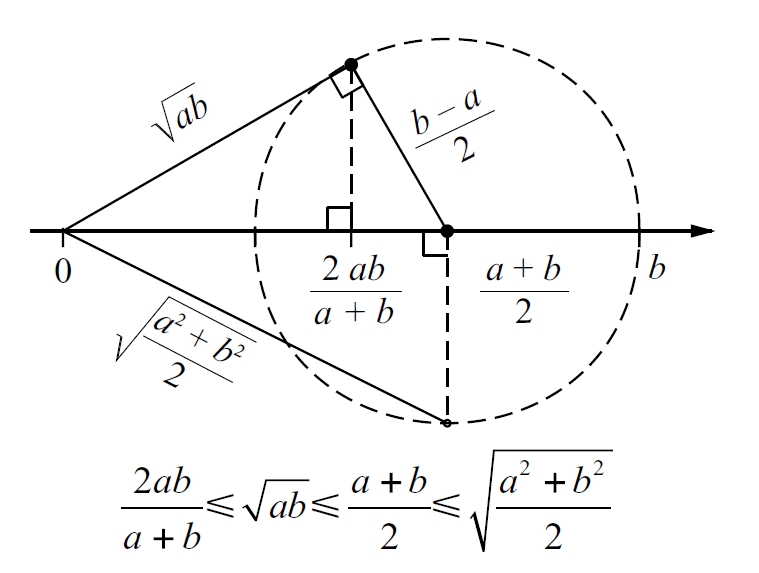
Mitjanes dels nombres a i b: harmònica, geomètrica, aritmètica i quadràtica
© fototeca.cat
Matemàtiques
Donats n valors o observacions x1, x2, ..., xn, valor x definit com la suma de tots ells dividida per llur nombre, és a dir, .
La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població , mentre que si les observacions són d’una mostra aleatòria de la població mostreig, x és la mitjana de la mostra A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n 1 , n 2 , , n k i freqüències respectives f 1 , f 2 , , f k , la fórmula per al càlcul de la mitjana és…