Resultats de la cerca
Es mostren 5 resultats
paràbola
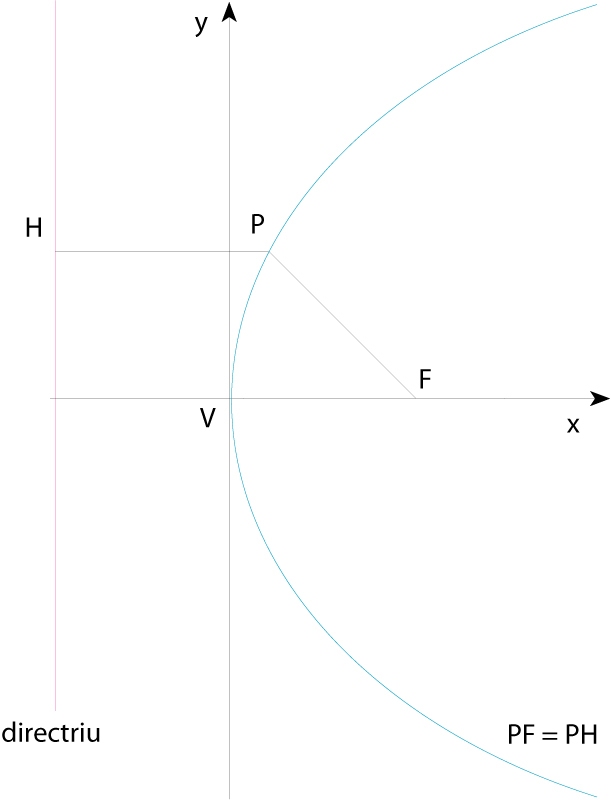
Paràbola (V vèrtex, F focus, P punt qualsevol de la paràbola)
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’una superfície cònica amb un pla paral·lel a una de les generatrius.
Constitueix el lloc geomètric dels punts del pla que equidisten d’un punt el focus de la paràbola i d’una recta que no conté el punt la directriu de la paràbola Té un eix de simetria que és la recta perpendicular que passa pel focus i que talla la paràbola en un punt anomenat vèrtex Referida a l’eix de simetria i a la seva perpendicular pel vèrtex, l’equació de la paràbola és y 2 =2 px , on p és la distància entre focus i directriu, anomenada paràmetre de la paràbola Hom pot demostrar que la gràfica de tota funció polinòmica de segon grau y= ax 2 + bx+ c és una paràbola de…
mediatriu
Matemàtiques
Donat un segment, lloc geomètric dels punts del pla que equidisten de tots dos extrems del segment.
Coincideix amb la recta perpendicular al punt mitjà del segment Les tres mediatrius dels costats d’un triangle es tallen en un punt únic, anomenat circumcentre
bisectriu
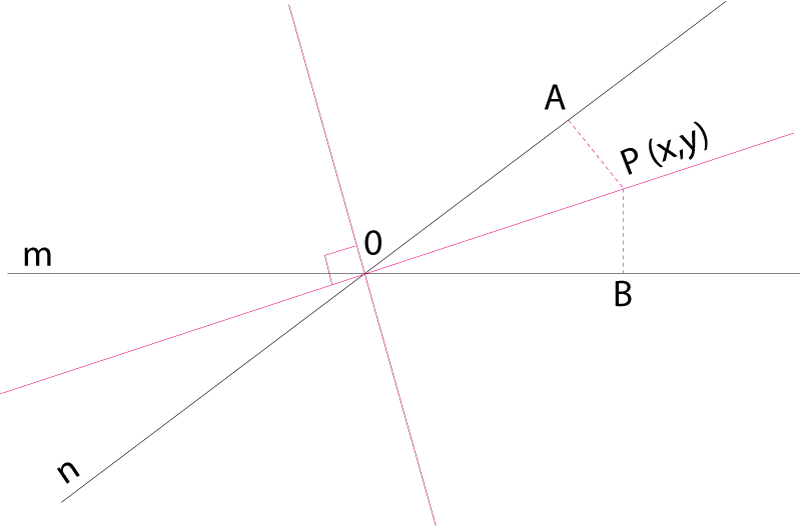
Bisectrius corresponents als quatre angles determinats per dues rectes que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels costats d’un angle, el qual divideix, per tant, en dos angles iguals.
Dues rectes que es tallen determinen quatre angles, iguals dos a dos Llurs bisectrius són dues rectes perpendiculars entre elles En considerar un dels quatre angles hom distingeix la bisectriu interior i la bisectriu exterior Les equacions de les bisectrius dels angles que determinen dues rectes que es tallen, les d’equacions de les quals són, en una referència cartesiana normal, A 1 x + B 1 y + C 1 = 0 i A 2 x + B 2 y + C 2 =0, són
bisector
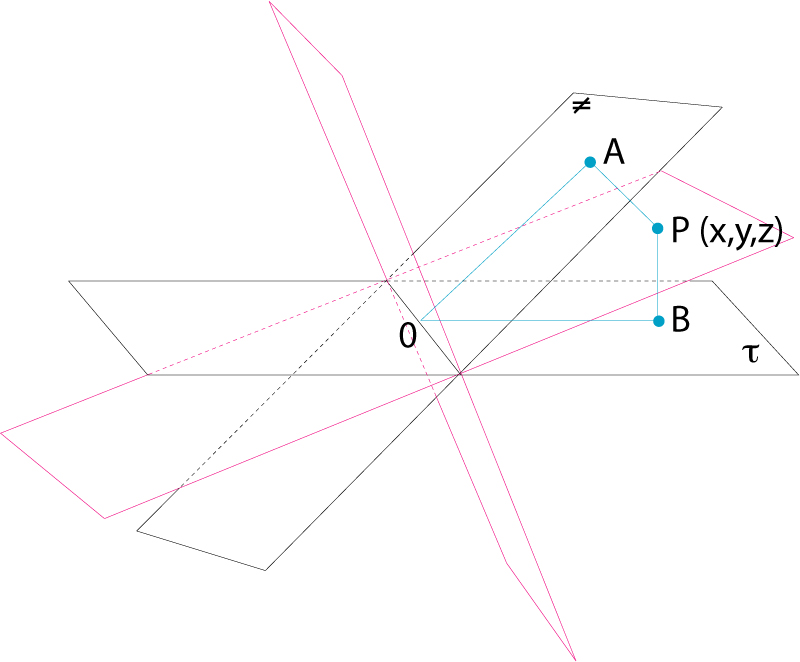
Plans bisectors dels quatre díedres formats per dos plans donats que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels dos plans costats d’un angle díedre, el qual, per tant, és dividit en dos díedres iguals.
Dos plans no parallels determinen quatre angles díedres, per als quals hom distingeix dos plans bisectors Per a cada díedre, un dels plans bisectors serà interior, i l’altre, exterior Si les equacions cartesianes de dos plans són A 1 x + B 1 y + C 1 z + D 1 = 0 i A 2 x + B 2 y + C 2 z + D 2 = 0, en una referència cartesiana normal, l’equació dels dos plans bisectors dels díedres que aquells determinen és
configuració simètrica
Matemàtiques
Configuració geomètrica tal que per a tot punt A de la configuració hi ha un altre punt B, anomenat simètric, els quals equidisten respecte a un element prefixat, que pot ésser un punt (centre de simetria), una línia (eix de simetria) o un pla (pla de simetria).
En aquests tres casos hom parla respectivament de simetria central, axial o especular simetria Aplicant simetries a una configuració qualsevol hom obté una nova configuració composta simètrica