Resultats de la cerca
Es mostren 6 resultats
problema dels set ponts de Königsberg
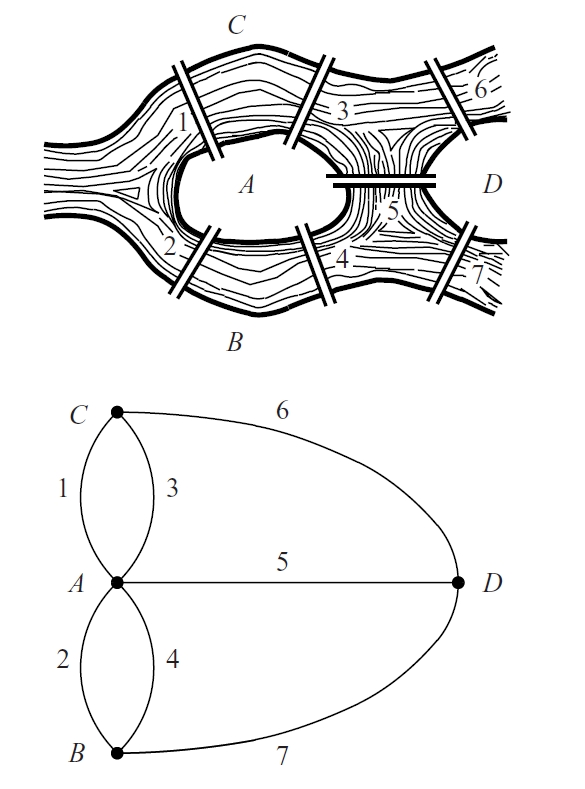
problema dels set ponts de Königsberg
Fototeca.cat
Matemàtiques
Problema la solució del qual s’associa sovint amb l’origen de la teoria de grafs.
La ciutat prussiana de Königsberg actualment Kaliningrad està dividida pel riu Pregol’a, que voreja l’illa de Kneiphof Hi havia set ponts disposats com s’indica a la figura Els habitants de la ciutat es plantejaven si era possible fer un recorregut tancat que passés una sola vegada per cadascun dels set ponts En llenguatge de teoria de grafs, la pregunta és si el graf és eulerià La resposta és negativa La solució del problema va ser trobada per Leonard Euler, el 1736, introduint per primer cop la noció de graf i resolent a la vegada un problema de caràcter més general
matroide
Matemàtiques
Estructura algèbrica consistent en un conjunt E i un conjunt S de parts no buides de E que satisfan: tot singletó de E pertany a S
.
Si X ∈S , aleshores tota part Y no buida de E inclosa en X pertany també a S i, per a tota part A de E , si X i Y són dos elements de S continguts en A i maximals, aleshores card X = card Y La teoria de matroides fou introduïda per Withney el 1935 i ha experimentat un desenvolupament ràpid en ésser aplicada als espais vectorials i a la teoria de grafs
graf
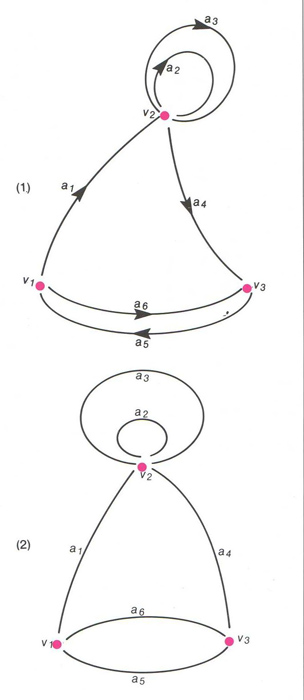
(1) Graf orientat: el camí ( a 1, a 2, a 4, a 5) és un circuit , els arcs a 2 i a 3 són bucles o rulls en el vèrtex v 2. i a 6 és un camí de v 1 a v 3. (2) graf no orientat: la cadena ( a 1, a 4, a 5) és un cicle , les arestes a 2 i a 3 són bucles o rulls en el vèrtex v 2, i a 6 és una aresta de v 1 a v 3.
© fototeca.cat
Matemàtiques
Ens constituït per un conjunt S
d’elements i per un conjunt C
de línies que uneixen els elements de S
(tot palesant una correspondència
de S
en si mateix).
Cal distingir entre un graf orientat i un graf no orientat Un graf orientat és una quaterna S, C, o, e , on S és el conjunt d’elements o vèrtexs, C és el conjunt de línies entre els vèrtexs o arcs, o és l' aplicació origen que assigna a cada arc el vèrtex del qual surt, i e és l' aplicació extrem que assigna a cada arc el vèrtex al qual arriba Un graf no orientat és una terna S, C, e , on S és el conjunt dels vèrtexs, C és el conjunt de línies entre els vèrtexs o arestes , i e és l’aplicació que assigna a cada aresta una parella de S × S , formada pels vèrtexs que uneix l’aresta en qüestió…
nombre de Folkman
Matemàtiques
Nombre emprat en teoria de grafs, representat per la notació 107, i el valor del qual és .
investigació operativa
Matemàtiques
Branca de les matemàtiques molt lligada a l’estadística i a l’anàlisi dels processos d’optimització, consistent a aplicar tècniques matemàtiques i estadístiques a la solució de problemes governamentals, empresarials, industrials, educatius, etc.
Les tècniques de la investigació operativa són particularment útils en l’equilibrament d’objectius conflictius amb un gran nombre de línies d’acció alternatives, amb conflictes d’interessos i amb un gran nombre de variables complexes i interaccionants La investigació operativa s’utilitza per a conduir i coordinar les operacions o les activitats dins un sistema organitzat empresa, administració pública, etc, i els estudis que en són el resultat intenten proporcionar a l’executiu una base sòlida, científica i quantitativa per a la presa de decisions Es caracteritza també per l’aplicació del…