Resultats de la cerca
Es mostren 17 resultats
anàlisi harmònica
Matemàtiques
Representació de funcions periòdiques mitjançant sumació i integració de desenvolupaments en sèrie d’algunes funcions trigonomètriques elementals.
Permet d’obtenir expressions senzilles aproximades de les funcions i deduir propietats generals a partir de les propietats particulars d’aquelles funcions elementals
funció harmònica
Matemàtiques
Funció f:ℝ n →ℝque és solució de l’equació de Laplace, és a dir que satisfà Δf≡∇2 f=∂2 f/∂x1 2 +...+∂2 f/∂xn 2 =0.
A més a més hom exigeix, generalment, que f sigui definida en un obert U ⊂ℝ n que hi sigui contínuament diferenciable dues vegades
progressió harmònica
Matemàtiques
Progressió en què cada terme ak , és l’invers del terme corresponent d’una progressió aritmètica, bk : ak =1/bk
.
divisió harmònica
Matemàtiques
Conjunt de dues parel·les de punts A,B i C,D d’una mateixa recta tals, que els dos punts d’una mateixa parel·la divideixen el segment format pels dos altres punts en les raons oposades AC/AD = BC/BD.
Cada punt d’aquesta divisió és anomenat conjugat harmònic del seu associat respecte als altres dos
mitjana
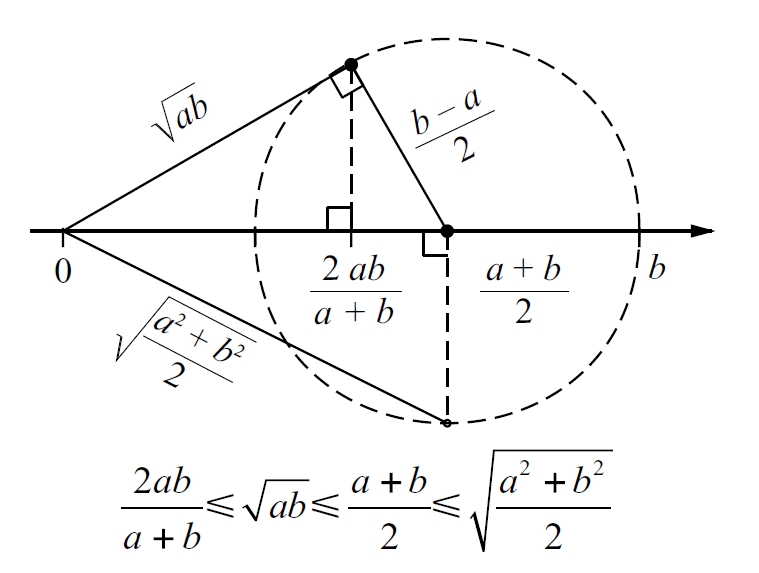
Mitjanes dels nombres a i b: harmònica, geomètrica, aritmètica i quadràtica
© fototeca.cat
Matemàtiques
Donats n valors o observacions x1, x2, ..., xn, valor x definit com la suma de tots ells dividida per llur nombre, és a dir, .
La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població , mentre que si les observacions són d’una mostra aleatòria de la població mostreig, x és la mitjana de la mostra A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n 1 , n 2 , , n k i freqüències respectives f 1 , f 2 , , f k , la fórmula per al càlcul de la mitjana és…
Charles Fefferman

Charles Fefferman
Matemàtiques
Matemàtic nord-americà.
Professor a la Universitat de Chicago, el 1978 li fou atorgada la medalla Fields per diverses innovacions en anàlisi clàssica, útils en l’estudi de la interfície entre anàlisi harmònica, anàlisi complexa i les equacions diferencials
Nicòmac de Gerasa
Matemàtiques
Matemàtic grec.
El seu llibre Introducció a l’aritmètica , d’inspiració pitagòrica, fou considerat durant tota l’edat mitjana un dels més típics representants de la ciència grega Escriví també un Manual d’harmònica , que tingué una àmplia difusió dins el món medieval
Paul Joseph Cohen
Matemàtiques
Matemàtic nord-americà.
Professor a la Universitat de Stanford des del 1961, provà la impossibilitat de la demostració d’hipòtesis contínues a partir del conjunt d’axiomes d’una teoria Estudià les equacions diferencials parcials i l’anàlisi harmònica El 1966 li fou atorgada la medalla Fields
Jean Baptiste Joseph Fourier
Matemàtiques
Matemàtic francès.
Fou professor d’anàlisi matemàtica a l’École Polytechnique 1795 de París Estudià la propagació de la calor, i publicà Théorie analytique de la chaleur 1822 Fruit d’aquest treball fou el desenvolupament de les sèries matemàtiques que duen el seu nom i que constitueixen la base de l’anàlisi harmònica anàlisi de Fourier Fou nomenat secretari perpetu de l’Académie des Sciences el 1822 i membre de l’Académie Française el 1826
Norbert Wiener
Matemàtiques
Matemàtic nord-americà.
Estudià a Harvard, Cambridge i Göttingen Fou nomenat professor de lògica matemàtica al MIT 1932 Hom el considera el creador de la cibernètica , les bases de la qual exposà en l’obra Cybernetics 1948, les quals han donat lloc posteriorment a un gran nombre d’aplicacions Poc després publicà Human Use of Human Beings Cybernetics and Society 1950, que ha estat traduïda al català Cibernètica i Societat , 1969, i I am a Mathematician 1956 Són notables, també, les seves recerques sobre teoria de probabilitats, integrals de Fourier, anàlisi harmònica, espais vectorials, moviment brownià…