Resultats de la cerca
Es mostren 12 resultats
Reial Acadèmia de Ciències i Arts de Barcelona

Emblema de la Reial Acadèmia de Ciències i Arts de Barcelona
© Fototeca.cat
Entitats culturals i cíviques
Matemàtiques
Astronomia
Física
Química
Geologia
Biologia
Tecnologia
Institució fundada l’any 1764 amb el nom de Conferència Fisicomatemàtica Experimental amb Francesc Subiràs com a president i Josep Anton Desvalls, marquès de Llupià, com a secretari, limitada inicialment a 16 membres.
Celebrà les primeres reunions a la rebotiga d’una farmàcia i més tard a unes golfes del carrer de la Boqueria, on fou installat un gabinet de màquines d’experimentació El desembre del 1765 es reorganitzà amb el nom de Reial Conferència Física , amb uns nous estatuts pels quals fou designat president el capità general de Catalunya, i amplià el seu abast al conreu de “totes les ciències naturals i l’avenç de les arts útils”, amb nou seccions àlgebra i geometria estàtica i hidroestàtica electricitat magnetisme i òptica pneumàtica i acústica història natural botànica química agricultura El 1770…
corba de Peano
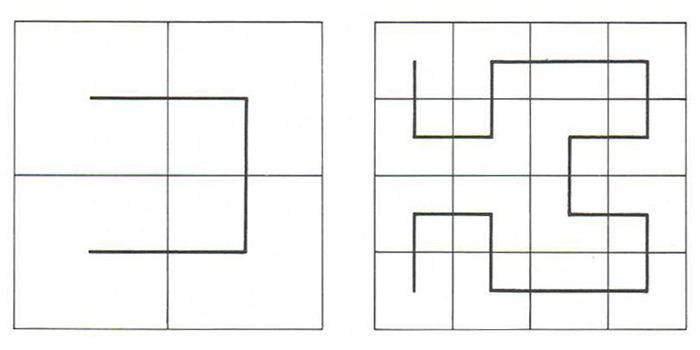
Corba de Peano traçada unint els punts centrals dels successius quadrats en què hom divideix el quadrat inicial
© fototeca.cat
Matemàtiques
Donat un quadrat, corba que, amb una longitud finita des del seu començament, ateny qualsevol punt del quadrat inicialment fixat.
Abraham Wald
Matemàtiques
Matemàtic hongarès, d’origen jueu.
Estudià a Viena amb KMenger Es dedicà inicialment a la geometria i després s’interessà per l’econometria A causa de l’ocupació d’Àustria pels nazis, anà als EUA 1938, on treballà en estadística per a l’exèrcit nord-americà És el creador de la moderna teoria de la decisió estadística 1949 Morí d’accident d’aviació
René Maurice Fréchet
Matemàtiques
Matemàtic probabilista francès.
Dedicat inicialment a l’estudi dels espais abstractes, reestructurà certs capítols de les matemàtiques per mitjà d’alguns axiomes emprant el llenguatge de la geometria distància, separació, entorn Encarregat per Borel de l’ensenyament del càlcul de les probabilitats a Estrasburg, s’especialitzà en aquesta teoria i esdevingué un dels capdavanters de la presentació axiomàtica de la probabilitat publicà obres sobre la noció de variable aleatòria i les formes de convergència de la teoria de les probabilitats i sobre les probabilitats en cadena
teoria de categories
Matemàtiques
Teoria introduïda cap al 1940 pels matemàtics S. Eilenberg i S. MacLane, fonamentada sobre el concepte de categoria, i aplicada inicialment en la topologia algèbrica.
És utilitzada en tot aquell tipus de problema algèbric on hom té una estructura de base i un conjunt de propietats genèriques que no depenen de la realització en un objecte matemàtic concret, especialment en àlgebra homològica i geometria algèbrica
Societat Catalana de Ciències Físiques, Químiques i Matemàtiques
Matemàtiques
Filial de l’Institut d’Estudis Catalans, creada l’any 1932 amb la finalitat d’agrupar científics de diferents activitats.
Inicialment, reuní membres de la revista Ciència , vinculats a la Societat Catalana de Química, que es dissolgué en crear-se la filial corresponent, i científics del Servei Meteorològic de Catalunya Josep Estalella en fou el primer president El succeí Eduard Fontserè en els períodes 1933-35 i 1936-39, que en mantingué el caliu, com a president de la Secció de Ciències de l’Institut, fins el 1959, en què s’iniciaren de nou les activitats a la clandestinitat amb una nova junta presidida per AEsteve i Subirana Entre les seves activitats destacaren els cursos organitzats en…
Vicent Caselles i Costa
Matemàtiques
Matemàtic.
Llicenciat per la Universitat de València, amplià estudis a les universitats de Tübingen i Besançon Professor, successivament, a la Universitat de les Illes Balears 1994 i a la Universitat Pompeu Fabra 1999, d’on esdevingué catedràtic el 2002, és autor d’uns 200 treballs publicats que el convertiren en el matemàtic de l’Estat espanyol més citat internacionalment Inicialment, es dedicà a l’anàlisi funcional i, posteriorment, al processament digital d’imatges i el seu tractament per ordinador, matèries en les quals esdevingué un referent internacional De les seves publicacions hom pot esmentar…
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament,…
fiabilitat
Matemàtiques
Tecnologia
Mesura de la confiança que hom pot tenir en el funcionament correcte d’un sistema o d’un dels elements que el componen.
Hom l’expressa per la probabilitat que s’acompleixi aquest funcionament correcte durant un temps determinat i en condicions especificades de funcionament La fiabilitat variarà amb aquestes condicions, tant si són pròpies del sistema com si són externes Hom pot estudiar la fiabilitat d’un element i la del sistema en el seu conjunt en funció del temps mitjançant tres nocions interrelacionades la supervivència, la duració de vida i la probabilitat condicional de falliment o d’avaria, la més instructiva de les quals és la tercera amb un nombre suficient d’observacions hom obté, per a aquesta…
atzar
Matemàtiques
Conjunt de causes inconegudes que produeixen un efecte no previsible; un fenomen és atribuïble a l’atzar, o és fortuït o és aleatori, quan no és ni inevitable ni impossible.
Una característica important d’aquests fenòmens és que llur realització depèn d’un conjunt de condicions massa complexes per a poder-les conèixer i estudiar totes Un esdeveniment que apareix inevitablement quan es produeix un conjunt de condicions és un esdeveniment cert respecte a aquestes hom anomena impossibles els que mai no poden aparèixer Els esdeveniments fortuïts són els que tant poden donar-se com no donar-se si es realitzen les condicions és a dir, si aquestes no reflecteixen del tot les condicions necessàries i suficients perquè es realitzi l’esdeveniment, i es tracta…