Resultats de la cerca
Es mostren 9 resultats
derivada d’una funció en un punt
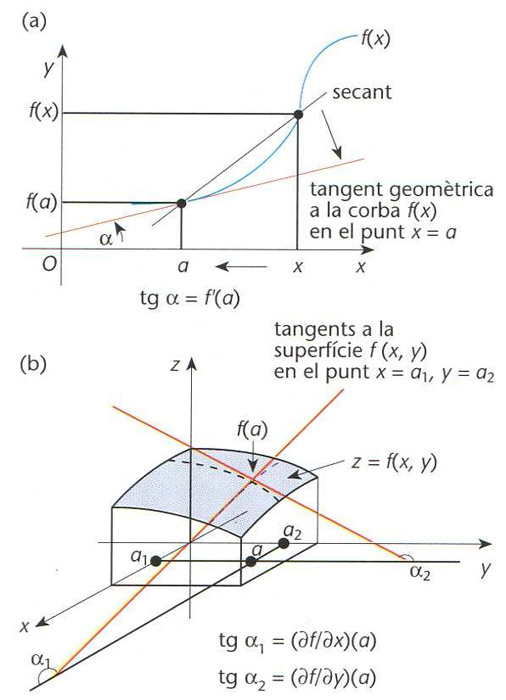
Interpretació gràfica de la derivada d’una funció (a) i de les derivades parcials d’una funció de dues variables (b); en (a), tgα = f' (a); en (b), tgα1 = ϑf/ϑx (a) i tgα2 = ϑf/ϑy (a)
© fototeca.cat
Matemàtiques
Donada una funció f: D⊂ℝ→ℝ i un punt del seu domini de definició, a ∈D, límit, si existeix del quocient [f(x) — f(a)]/(x-a) quan x tendeix a a tot mantenint-se a l’interior de D.
Quan aquest límit existeix, hom diu que la funció f és derivable en a , i el límit és notat per f´ a , df/dx a o Df a , i hom l’anomena derivada de f en el punt a Hom diu que f és derivable en un cert domini S si ho és a cada punt de S Aleshores, la funció f´ x que assigna a cada punt a ∈ S la derivada de f en a és anomenada funció derivada de f o, simplement, derivada de f Si f´ x és, al seu torn, derivable en un cert domini T , hom pot definir-n'hi la derivada, que és la derivada segona de f, f´´ x Hom procedeix consecutivament per tal de definir les derivades d’ordre…
Georges-Henri Lemaître
Astronomia
Matemàtiques
Astrofísic i matemàtic belga.
Estudià especialment la relativitat general d’Einstein i les seves aplicacions en cosmologia, la recessió de les galàxies i la seva interpretació dintre la teoria de l’univers en expansió, avançant-se així a la hipòtesi coneguda com a model del big-bang Entre les seves obres es destaquen Discussion sur l’évolution de l’Univers 1933 i Hypothèse de l’atome primitif 1946
Lewis Carroll
Literatura anglesa
Matemàtiques
Pseudònim del matemàtic i escriptor anglès Charles Lutwidge Dodgson.
Professor de matemàtiques a Oxford, publicà moltes obres científiques Escriví narracions pseudoinfantils que, tot i que la matèria narrativa sembla abocada a l’absurd, són susceptibles d’interpretació La seva obra més coneguda és Alícia al país de les meravelles 1865 Altres contes seus són Through the looking-glass ‘A través del mirall’, 1872, Sylvie and Bruno 1889, The Hunting of the Snark ‘La cacera del Snark’, 1876
Hermann Minkowski
Matemàtiques
Matemàtic lituà.
Fou professor a Zuric i a Göttingen El 1882 guanyà el premi de l’Académie des Sciences de París per la publicació d’una memòria on establí les bases de la teoria de les formes quadràtiques amb coeficients enters Féu investigacions sobre geometries no euclidianes i donà una interpretació geomètrica de la relativitat especial d’Einstein mitjançant un espai de quatre dimensions, que porta el seu nom Entre les seves obres cal destacar Raum und Zeit ‘Espai i temps’, 1907 i Zwei Abhandlungen über die Grundleichungen der Elektrodynamik ‘Dos manuals sobre fonaments de l’electrodinàmica…
William Kingdon Clifford
Filosofia
Matemàtiques
Matemàtic i filòsof anglès.
A partir d’una generalització dels treballs sobre els quaternions de William Rowan Hamilton, el 1872 introduí un nou tipus de nombres complexos, els biquaternions, que aplicà fonamentalment a l’estudi de les geometries no euclidianes Estudià les estructures topològiques de l’espai i suggerí que la matèria és un tipus particular de curvatura de l’espai, amb la qual cosa prefigurava la teoria de la relativitat general d’Einstein, i explicità les dificultats que les geometries no euclidianes presenten a la teoria de les proposicions sintètiques ‘a priori' de Kant Com a filòsof, pertany en certa…
integral
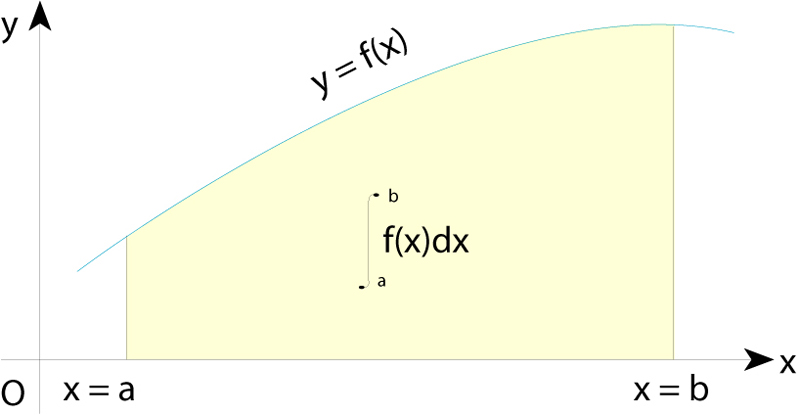
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b , hom determina en cada subinterval x i - 1 , x i…
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F quocient, el…
àlgebra

Triàngle numèric, més tard conegut com a triangle de Pascal, d’un manuscrit xinès del 1303
© Fototeca.cat
Matemàtiques
Branca de les matemàtiques que estudia les estructures algèbriques dels conjunts.
Hom l’aplica, per tant, en les situacions on hi ha un conjunt ben definit i una noció clara d’operació entre els seus elements operació interna o entre aquests i els elements d’altres conjunts operació externa L’àlgebra ha evolucionat des de l’interès inicial per a resoldre problemes fonamentalment pràctics fins al desenvolupament del mètode abstracte Dues inclinacions diferents han desembocat en l’àlgebra moderna D’una banda, l’ àlgebra clàssica , simple instrument per a fer càlculs i resoldre equacions que usava només els conceptes immediats que hom reconeixia al problema les quantitats…