Resultats de la cerca
Es mostren 15 resultats
e
Matemàtiques
Nombre irracional i transcendent definit per
.
Els primers coeficients de la seva expressió decimal illimitada són e= 2,7182818284590 És el límit de la sèrie i és relacionat amb els altres nombres fonamentals de la matemàtica per l’expressió e iπ +1 = 0 La funció de ℝen ℝdefinida per x → e x és la funció exponencial,i la definida per és la funció logarítmica , que assigna a cada nombre real el seu logaritme natural o neperià El nombre e i les funcions associades són de gran interès i utilitat en física i matemàtiques
incommensurable
Matemàtiques
Dit de dues magnituds el quocient entre les quals no és un nombre racional.
El quocient defineix, doncs, un nombre irracional
fracció contínua
Matemàtiques
Expressió de la forma
on l’algorisme s’estén indefinidament.
Hom l’expressa abreujadament mitjançant la notació a 0 + a 1 / b 1 + a 2 / b 2 + a 3 / b 3 + Són emprades per a representar nombres irracionals Així, si α 0 és un nombre irracional positiu, i n ≥0, α 0 admet l’expressió on u n és la part entera de α i α n ≥1 és definit per la relació de recurrència α n - 1 = u n - 1 + 1/α n , n≥1 La successió u n n ≥ 0 és el desenvolupament de α 0 en fracció contínua , i els coeficients u n són els quocients incomplets de la fracció contínua Un exemple d’aquest tipus de desenvolupament és el del nombre π/4, fet per William Brouncker
Euclides
Matemàtiques
Matemàtic grec.
Estudià probablement a Atenes i residí a Alexandria, on fundà una escola matemàtica Desenvolupà les seves teories en els Elements , en 13 volums Donà un tractament lògic a la geometria i la dotà d’un cos d’axiomes i de postulats que feren que fos considerada l’única geometria possible durant 19 segles, fins a l’aparició de geometries no euclidianes, les quals no segueixen els seus postulats Estudià les fraccions i les proporcions i enuncià una teoria dels nombres Demostrà que la sèrie de nombres primers és indefinida i que és un nombre irracional Ideà un procés de càlcul per a…
nombre real
Matemàtiques
Cadascun dels nombres que hom pot obtenir en mesurar magnituds contínues.
Hom obté el conjunt dels nombres reals completant el conjunt dels nombres racionals amb tots els nombres irracionals que poden ésser representats sobre la recta, tals com etc La manera més simple d’introduir teòricament i d’utilitzar en la pràctica els nombres reals és per mitjà de llur expressió decimal Tot nombre real és expressat en forma decimal amb infinites xifres que, en el cas dels nombres irracionals, no es repeteixen periòdicament Això suposa que per a definir un nombre real cal donar una llei que permeti d’obtenir tantes xifres decimals com hom vulgui A la pràctica, però, hom pren…
nombre de Feigenbaum
Matemàtiques
Nombre irracional, descobert pel matemàtic Mitchell Feigenbaum el 1975, d’utilitat comparable als nombres e, π i C (nombre d’Euler).
El seu valor és δ = 4,669 201 609 10
número d’or
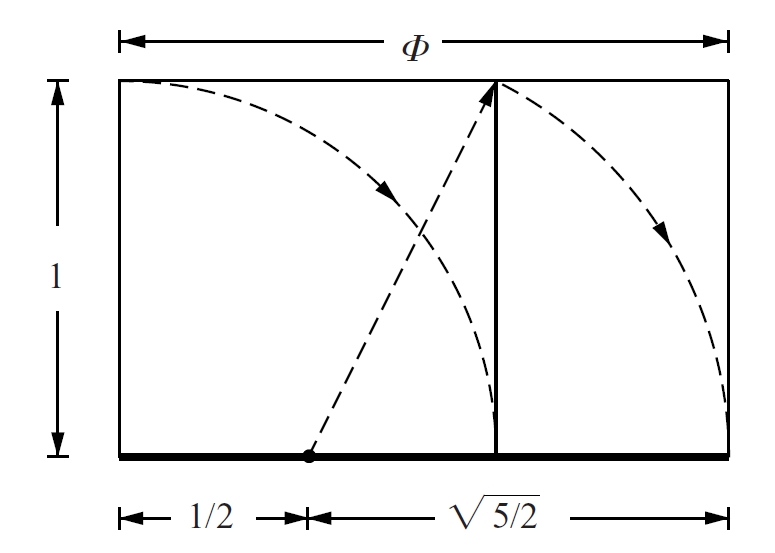
número d’or
Matemàtiques
Nombre irracional algebraic positiu que, elevat al quadrat, és igual a ell mateix més una unitat: (1 + ⎷5 ) ⁄ 2 = 1,618.
El número d’or apareix en molts problemes geomètrics relatius a les divisions harmòniques de segments o a proporcions de rectangles, o entre mides Així, un rectangle té de proporció el número d’or si, i solament si, té la mateixa proporció del rectangle que resulta de treure del rectangle original un quadrat Aquest nombre és el límit dels quocients 1 ⁄ 1, 2 ⁄ 1, 3 ⁄ 2, 5 ⁄ 3 dels termes de la successió de Fibonacci i té una important presència en elements naturals i artístics, especialment en pintura i arquitectura, ja que que el número d’or és igual al cosinus de 36º i, per tant, està lligat…