Resultats de la cerca
Es mostren 87 resultats
arrel d’un polinomi
Matemàtiques
Donat un polinomi p(x) amb coeficients en un anell o un cos K, element k de K tal que el valor numèric de p(x) en x = k és igual a 0, és a dir, tal que p(k) = 0.
L’element k és una arrel o zero d’un polinomi no nul p x si, i solament si, p x és divisible per x – k
homotècia
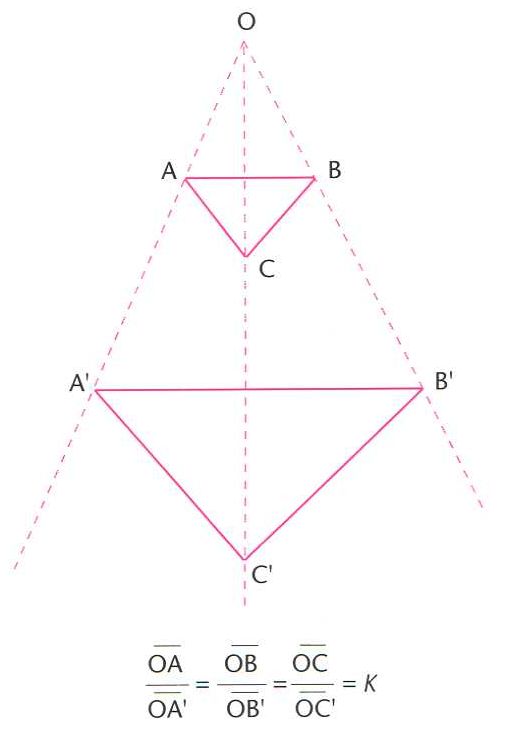
Homotècia, transformació homotètica d’un triangle ABC (O, centre de l’homotècia; k, raó d’homotècia)
© Fototeca.cat
Matemàtiques
Transformació geomètrica del pla o de l’espai que compleix aquestes dues condicions.
Qualsevol punt A i la seva imatge A' són alineats amb un punt fix O anomenat centre d’homotècia , i els segments compleixen la relació k essent, per a cada homotècia, una constant real anomenada raó de l’homotècia Les homotècies transformen rectes en rectes, circumferències en circumferències i conserven els angles
matriu
Matemàtiques
Disposició dels elements d’un cos K
de la manera següent
.
Segons que el cos K sigui el dels nombres reals o el dels nombres complexos, hom parla de matriu real o de matriu complexa , respectivament Cadascuna de les línies horitzontals de nombres és una fila de la matriu, i cada línia vertical de nombres n'és una columna En l’exemple donat, la matriu A té files i columnes hom diu que A és una matriu m × n El conjunt de les matrius m ×és notat per M m X n K Una matriu pot ésser expressada també mitjançant el seu element genèric a i j , en la forma A = a i j Aquí, és l' índex de fila i j és l' índex de columna La fila…
distribució gamma
Matemàtiques
Llei de probabilitat de la variable contínua x, la funció de densitat de la qual és f(x) = e- xxk - 1/Γ(k) (0 < x < ∞;k > 0).
D’aquesta llei deriven algunes expressions particulars, com la llei X 2 i la llei d’Erlang Tendeix cap a la llei normal quan k augmenta indefinidament
subcòs
Matemàtiques
Qualsevol subconjunt L d’un cos K tal, que és estable per les dues operacions de K i, mitjançant aquestes restriccions, L té també una estructura de cos.
L és subcòs del cos K si L és un subanell unitari tal, que l’invers de tot element no nul de L pertany a L El conjunt de nombres racionals és un subcòs del conjunt de nombres reals el qual té estructura de cos
deltoide
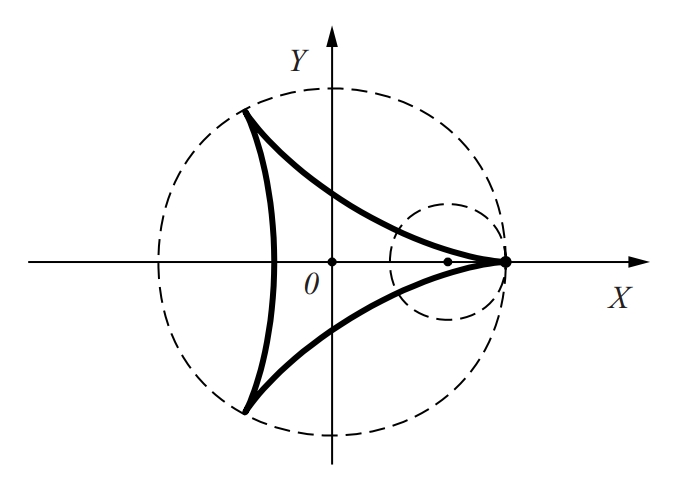
deltoide
Matemàtiques
Hipocicloide d’un cercle de radi k que roda, sense lliscar, dintre d’un altre que té el radi triple.
Les seves equacions paramètriques són x = k 2cos t + cos 2t , i y = k 2sin t + sin 2 t
mètode dels multiplicadors de Lagrange
Matemàtiques
Mètode per a trobar els màxims o mínims d’una funció u = F(x1, x2,..., xn) de n variables, les quals són sotmeses a k condicions suplementàries φ1(x1, x2,..., xn) = 0, φ2(x1, x2,..., xn) = 0,..., φk(x1, x2,..., xn) = 0.
, x n = 0, φ 2 x 1 , x 2 ,, x n = 0,, φ k &x 1 , x 2 ,, x n = 0 El mètode consisteix a formar la funció + λ 2 φ 2 x 1 ,, x n + λ 2 φ 2 > x 1 ,, x n , + + λ k φ k x 1 ,, x n , on λ 1 ,, λ k són constants indeterminades, anomenades multiplicadors de Lagrange les n derivades parcials de ϕ igualades a 0 juntament amb les k condicions constitueixen un sistema de n + k equacions i n + k incògnites λ 1 ,, λ k , x 1 , , x n Atès que aquest sistema constitueix només una condició…
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F…
cargol de Pascal
Matemàtiques
Corba plana, tancada i simètrica respecte a l’eix X, l’equació de la qual és, en coordenades polars, r = 2a cosφ + K.
Presenta tres formes, segons que sigui 0 < K < 2 a cargol hiperbòlic , amb un llaç d’origen, K > 2 a > 0 cargol ellíptic , en el qual ha desaparegut el llaç a causa de l’existència d’un punt conjugat o K = 2 a cardioide El cargol de Pascal és una concoide d’una circumferència respecte a un dels seus punts Fou descrit per Étienne Pascal, pare de Blaise Pascal