Resultats de la cerca
Es mostren 4 resultats
cargol de Pascal
Matemàtiques
Corba plana, tancada i simètrica respecte a l’eix X, l’equació de la qual és, en coordenades polars, r = 2a cosφ + K.
Presenta tres formes, segons que sigui 0 < K < 2 a cargol hiperbòlic , amb un llaç d’origen, K > 2 a > 0 cargol ellíptic , en el qual ha desaparegut el llaç a causa de l’existència d’un punt conjugat o K = 2 a cardioide El cargol de Pascal és una concoide d’una circumferència respecte a un dels seus punts Fou descrit per Étienne Pascal, pare de Blaise Pascal
foli de Descartes
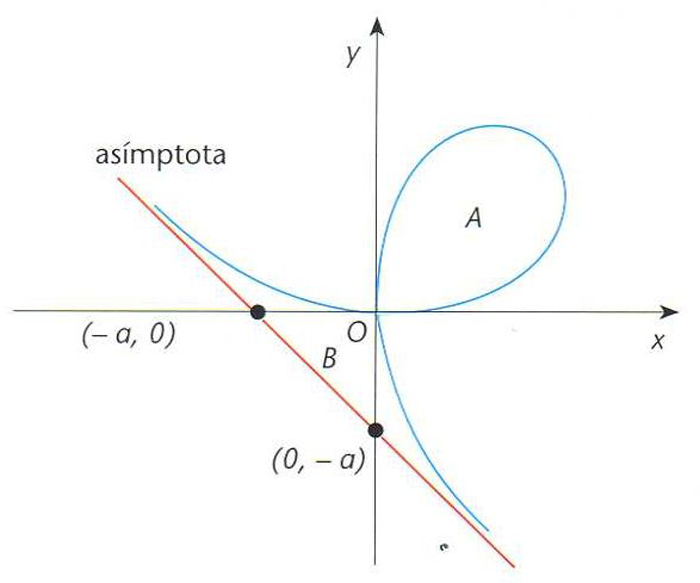
Foli de Descartes
© fototeca.cat
Matemàtiques
Cúbica expressada implícitament per l’equació cartesiana x3+y3=3axy, on a és una constant.
En forma paramètrica és expressada per x=3at|1+t 3 i y=3at 2 |1+t 3 La recta traçada pels punts de coordenades - a , 0 i 0, -a és una asímptota de la corba L’àrea A limitada pel llaç és igual a l’àrea B compresa entre les dues branques infinites i la asímptota esmentada
concoide d’una corba respecte a un punt
Matemàtiques
Donada una corba C
i un punt O
del seu pla, lloc geomètric dels punts Q
i Q’
determinats en mesurar, a ambdós costats, una determinada distància b
a partir del punt P
obtingut en tallar la corba C
mitjançant una recta R
que passi per O
.
De la definició resulta palès que la concoide d’una corba té dues branques Si C és una recta, i hom escull un sistema de coordenades polars amb origen al punt O , separat de C per una distància perpendicular a , l’expressió de la concoide de la recta C respecte a O és r= a/cos θ+ b si a < b es determina un llaç en O , si a = b hi ha una cúspide en O i la concoide és la concoide de Nicomedes , i si a > b no hi ha cúspide però hi ha un acnode en O Un altre cas particular s’escau quan C és una circumferència en aquest cas, la concoide de la circumferència C respecte a un…
concoide
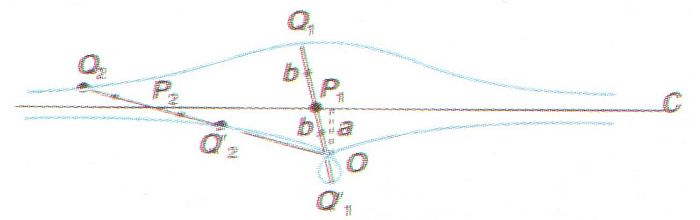
Concoide d’una recta C respecte a un punt O, en el cas de formació d’un llaç en O(a major que b); es satisfà que P2Q2 = P2Q2' = b = P1Q1 = P1Q1'
©
Matemàtiques
Corba plana d’equació x2 y2=(a+y2 ) (b2- y2 ), on a i b són dues constants.