Resultats de la cerca
Es mostren 15 resultats
valoració
Matemàtiques
Aplicació f d’un reticle (R, ∨, ∧) en el conjunt de nombres reals tal que f(A ∨B) + f(A ∧B) = f(A) + f(B).
Les probabilitats, les longituds, les àrees, els volums, etc, són exemples usuals de valoracions
ortòedre
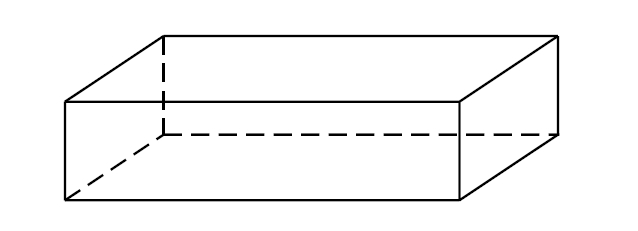
Ortòedre
Matemàtiques
Prisma de sis cares rectangulars que té tots els angles rectes.
Si les longituds de les arestes són a, b i c , la fórmula del volum de l’ortòedre és V=abc
Johann Jakob Balmer
Física
Matemàtiques
Matemàtic i físic suís, educat a Basilea, on fou professor de la universitat.
El 1885 obtingué empíricament la fórmula que determina les longituds d’ona de les ratlles de la sèrie de Balmer , fórmula que, interpretada per Niels Bohr, inspirà l’antiga teoria quàntica
Heró d’Alexandria
Matemàtiques
Matemàtic i inventor grec.
Establí una fórmula per a obtenir l’àrea d’un triangle sabent les longituds dels costats i un mètode aproximatiu per a calcular les arrels quadrades i cúbiques Trobà solucions algèbriques de les equacions de primer i segon grau i resolgué per mètodes aritmètics algunes equacions quadràtiques
evolvent
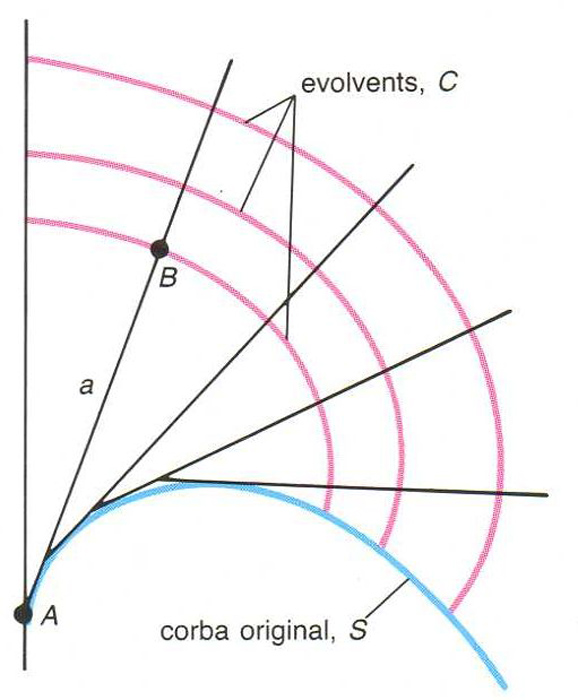
Les corbes C són les evovlents de S
© fototeca.cat
Matemàtiques
Donada una corba S
, cadascuna de les corbes ortogonals a les tangents de S
.
Si C és una envolvent de S , S és l'evoluta C Donada la corba S , hom pot generar una evolvent tot fixant una tangent a S en un punt de tangència A , limitant-ne la seva longitud a i anant-la enrotllant a la corba, de manera que el punt extrem B determina una evolvent Les diferents longituds a determinen les diferents evolvents
Giulio Carlo del Fagnano
Matemàtiques
Matemàtic italià.
Membre de la Royal Society 1723 Estudià el problema de la rectificació de l’ellipse i la paràbola, i en Opere mathematiche 1711-12 provà que, donada la diferència de longituds de dos arcs, hi havia infinites solucions per a determinar-los sobre aquestes corbes Euler es basà en els seus mètodes per a la demostració del teorema d’addició de les integrals ellíptiques
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar A partir de…
teorema de Pitàgores
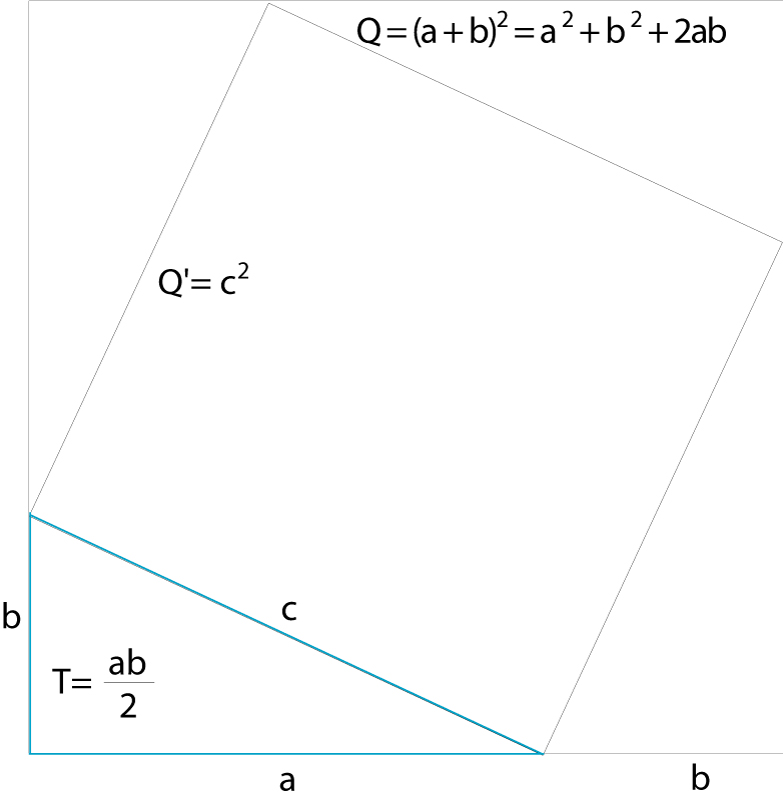
Matemàtiques
Teorema fonamental de la geometria segons el qual en un triangle rectangle l’àrea del quadrat que té per costat la hipotenusa és igual a la suma de les àrees dels quadrats que tenen per costat els catets.
Si a i b representen les longituds dels catets i c la longitud de la hipotenusa, el teorema Pitàgores és expressat per la igualtat c 2 = a 2 + b 2 Bé que la primera demostració del teorema sembla que fou feta pels membres de l’ escola pitagòrica Pitàgores vers l’any 550 aC, el teorema de Pitàgores, almenys en alguns casos particulars, ja era conegut pel poble egipci vers l’any 2000 aC, pels xinesos vers l’any 1100 aC i pels vedes vers l’any 800 aC D’altra banda, fou a partir del teorema que els pitagòrics descobriren que no n'hi ha prou amb els nombres enters i fraccionaris…
raó de semblança
Matemàtiques
Donades dues figures geomètriques semblants, raó entre les longituds dels elements corresponents.
La raó entre les àrees és el quadrat de la raó de semblança, mentre que la raó entre els volums és el cub de la raó de semblança
fórmula de Brahmagupta
Matemàtiques
L’àrea d’un quadrilàter de costats de longituds a, b, c i d és .