Resultats de la cerca
Es mostren 15 resultats
homofocal
Matemàtiques
Dit de les figures geomètriques que tenen els mateixos focus.
semblant
Matemàtiques
Dit dels termes algèbrics que contenen les mateixes lletres afectades dels mateixos exponents.
axioma d’extensibilitat
Matemàtiques
Axioma que afirma que dos conjunts són iguals si, i solament si, tenen els mateixos elements.
autòmat finit indeterminista
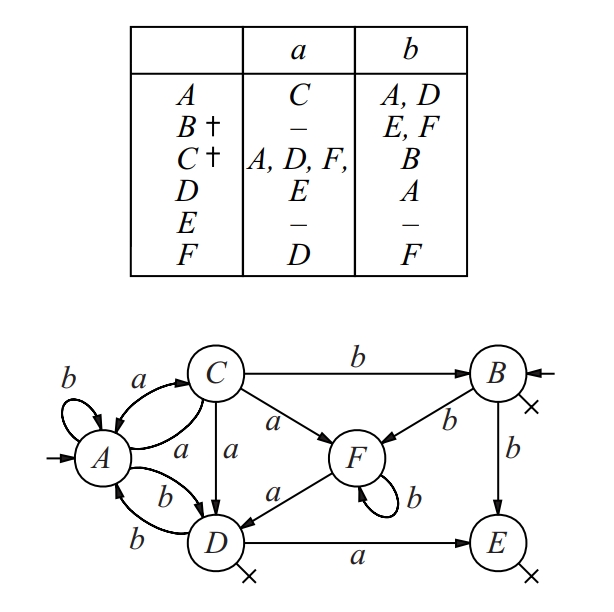
autòmat finit indeterminista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció
Georg Cantor

Georg Cantor
© Fototeca.cat
Matemàtiques
Matemàtic alemany.
Estudià a Zuric, Göttingen i Frankfurt, i es doctorà en filosofia a Berlín 1867 Fou professor a la Universitat de Halle Wittenberg des del 1872 al 1905 La seva obra abastà els camps de l’anàlisi, la topologia i la lògica matemàtica Creador de la teoria de conjunts, la seva anàlisi del concepte d’infinit ha plantejat la necessitat d’un examen crític dels mateixos fonaments de les matemàtiques Definí el concepte de cardinal per a conjunts finits i infinits Així mateix, desenvolupà la teoria dels nombres irracionals, introduí els nombres transfinits i definí, alhora que Julius…
atzar
Matemàtiques
Conjunt de causes inconegudes que produeixen un efecte no previsible; un fenomen és atribuïble a l’atzar, o és fortuït o és aleatori, quan no és ni inevitable ni impossible.
Una característica important d’aquests fenòmens és que llur realització depèn d’un conjunt de condicions massa complexes per a poder-les conèixer i estudiar totes Un esdeveniment que apareix inevitablement quan es produeix un conjunt de condicions és un esdeveniment cert respecte a aquestes hom anomena impossibles els que mai no poden aparèixer Els esdeveniments fortuïts són els que tant poden donar-se com no donar-se si es realitzen les condicions és a dir, si aquestes no reflecteixen del tot les condicions necessàries i suficients perquè es realitzi l’esdeveniment, i es tracta de fenòmens…
restricció d’una aplicació
Matemàtiques
Donats una funció f d’un conjunt A en un altre B i un subconjunt A’ de A, funció de A’ a, B que pren els mateixos valors que f per a tot element de A’
.
Hom l’anomena restricció de f al subconjunt A’