Resultats de la cerca
Es mostren 12 resultats
digraf
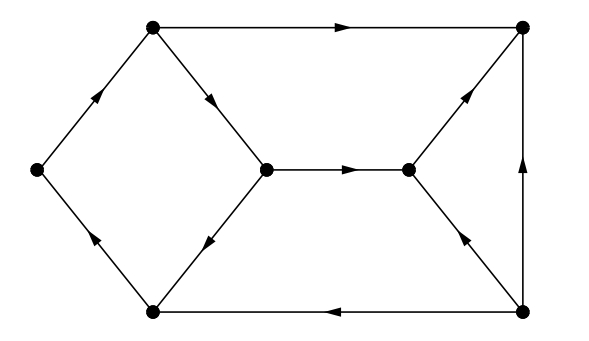
digraf
Matemàtiques
Graf les arestes del qual, anomenades arcs, són parells ordenats de vèrtexs diferents.
Un digraf G amb un conjunt de vèrtexs V i un conjunt d’arcs E es denota per G = V , E Sovint s’escriu també E = E G i V = V G
angle positiu
Matemàtiques
Angle generat pel moviment rotatori d’una semirecta en el sentit antihorari a partir d’una línia inicial i al voltant del vèrtex.
angle negatiu
Matemàtiques
Angle generat pel moviment rotatori d’una semirecta en el sentit horari a partir d’una línia inicial i al voltant del vèrtex.
graf
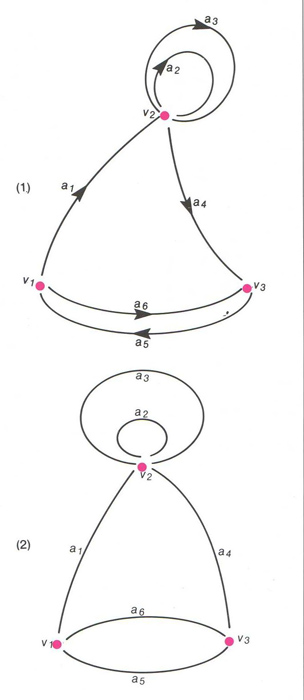
(1) Graf orientat: el camí ( a 1, a 2, a 4, a 5) és un circuit , els arcs a 2 i a 3 són bucles o rulls en el vèrtex v 2. i a 6 és un camí de v 1 a v 3. (2) graf no orientat: la cadena ( a 1, a 4, a 5) és un cicle , les arestes a 2 i a 3 són bucles o rulls en el vèrtex v 2, i a 6 és una aresta de v 1 a v 3.
© fototeca.cat
Matemàtiques
Ens constituït per un conjunt S
d’elements i per un conjunt C
de línies que uneixen els elements de S
(tot palesant una correspondència
de S
en si mateix).
Cal distingir entre un graf orientat i un graf no orientat Un graf orientat és una quaterna S, C, o, e , on S és el conjunt d’elements o vèrtexs, C és el conjunt de línies entre els vèrtexs o arcs, o és l' aplicació origen que assigna a cada arc el vèrtex del qual surt, i e és l' aplicació extrem que assigna a cada arc el vèrtex al qual arriba Un graf no orientat és una terna S, C, e , on S és el conjunt dels vèrtexs, C és el conjunt de línies entre els vèrtexs o arestes , i e és l’aplicació que assigna a cada aresta una parella de S × S…
segment
Matemàtiques
Part d’una recta compresa entre dos punts fixats, A
i B
, de la recta, que hom anomena extrems del segment
.
Quan aquests extrems són considerats en un cert ordre A, B , el segment és anomenat orientat o vector fix
base retrògrada
Matemàtiques
En un espai orientat, base pertanyent a l’orientació contrària ( base directa
).
símplex
Matemàtiques
Conjunt format per n + 1 punts p 0, p 1, ..., Pn linealment independents d’un espai euclidià de dimensió major que n i tots els punts de la forma x =λopo + λ 1p1 + ...
+ λ npn , on λ 0 + λ 1 + + λ n = 1 i 0 ≤λ i , per a cada i Els coeficients λ 0 , λ 1 , , λ n són anomenats coordenades baricèntriques del punt x , el qual pot ésser interpretat com el centre de masses de la distribució determinada en posar pesos λ 0 , λ 1 , , λ n en els punts p 0 , p 1 , , pi Aquest símplex és dit també n-símplex tancat , a fi de distingir-lo del n-símplex obert , en el qual totes les coordenades baricèntriques són estrictament positives Un símplex és degenerat si els punts determinants no són independents Els punts pi són dits vèrtexs i cada collecció de r + 1 vèrtexs…