Resultats de la cerca
Es mostren 3 resultats
secció
Matemàtiques
Intersecció d’un pla amb una superfície.
Si aquesta és una superfície cònica, hom parla de seccions còniques ellipses, hipèrboles i paràboles, parells de rectes, etc Les seccions produïdes en prismes i cilindres per plans perpendiculars, respectivament, a les arestes laterals i a les generatrius, són anomenades seccions rectes
Francesco Maurolico
Astronomia
Matemàtiques
Astrònom i matemàtic sicilià, conegut amb el nom de Francesco de Messina.
Fou monjo benedictí i traductor dels grans matemàtics grecs L’any 1543 publicà l’obra Cosmographia , i a partir de l’any 1550 es dedicà a l’estudi de l’òptica, especialment dels fenòmens relacionats amb els miralls esfèrics, els prismes i el mecanisme de la visió humana, investigacions que exposà en l’obra Photismi de homine 1611, en la qual també explicà el fenomen de l’arc de Sant Martí En el seu llibre Arithmeticorum libri duo 1575 utilitzà sistemàticament lletres en comptes de nombres en les deduccions matemàtiques, i també se serví àmpliament del tipus de raonament matemàtic…
políedre
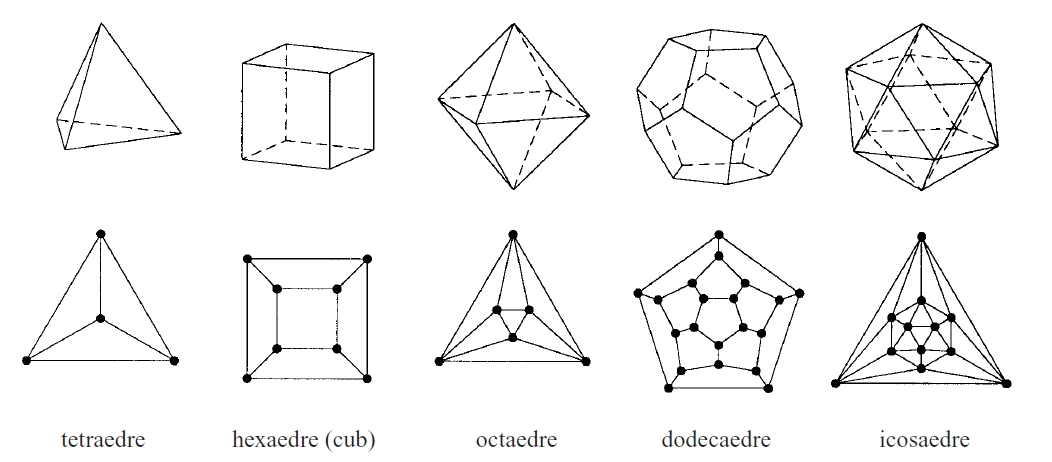
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
Matemàtiques
Sòlid limitat per quatre o més polígons anomenats cares.
Les interseccions de les cares constitueixen les arestes , i les interseccions de les arestes, els vèrtexs Un políedre és convex si qualsevol secció plana del políedre és un polígon convex Un políedre és còncau si no és convex Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars el tetràedre regular , l’ hexàedre regular o cub, l’ octàedre regular , el dodecàedre regular i…