Resultats de la cerca
Es mostren 16 resultats
procès estocàstic
Matemàtiques
Procés que estudia l’evolució d’un sistema (econòmic, biològic, tècnic, cibernètic, etc) en el qual la llei de probabilitat és funció del temps.
En rigor un procés estocàstic és una família de variables aleatòries {X t } , on t varia en un conjunt anomenat paramètric conjunt dels nombres naturals en el cas de processos discrets, un interval de la recta real en el cas de processos continus, etc
ergodicitat
Matemàtiques
Propietat d’un procés estocàstic en què tots els paràmetres probabilístics es poden determinar (amb probabilitat 1) d’una única funció qualsevol resultant del procés.
Aquesta propietat normalment s’expressa, també, dient que les mitjanes probabilístiques coincideixen amb les temporals En sentit ampli hom parla d’ergodicitat respecte a la mitjana, desviació típica o qualsevol altre paràmetre d’interès Els processos ergòdics són importants en el sentit que hom pot fer fàcilment mesures sobre una única funció resultant d’un fenomen físic, i aplicar els valors resultants a la teoria matemàtica dels processos estocàstics
simulació
Matemàtiques
Tècnica emprada en investigació operativa.
Consisteix a construir un model simbòlic d’un sistema o d’un procés complex, de manera que els seus elements siguin representats mitjançant els processos lògics i aritmètics que hom pot executar amb un programa d’ordinador, a fi d’estudiar el comportament del sistema i mesurar-ne les propietats dinàmiques, a base d’obtenir les característiques estadístiques del dit comportament Això permet d’avaluar i comparar diferents estratègies d’operació del sistema, sense que aquest existeixi realment Les aplicacions més conegudes d’aquesta tècnica han estat fetes en l’estudi de xarxes d’…
arbre
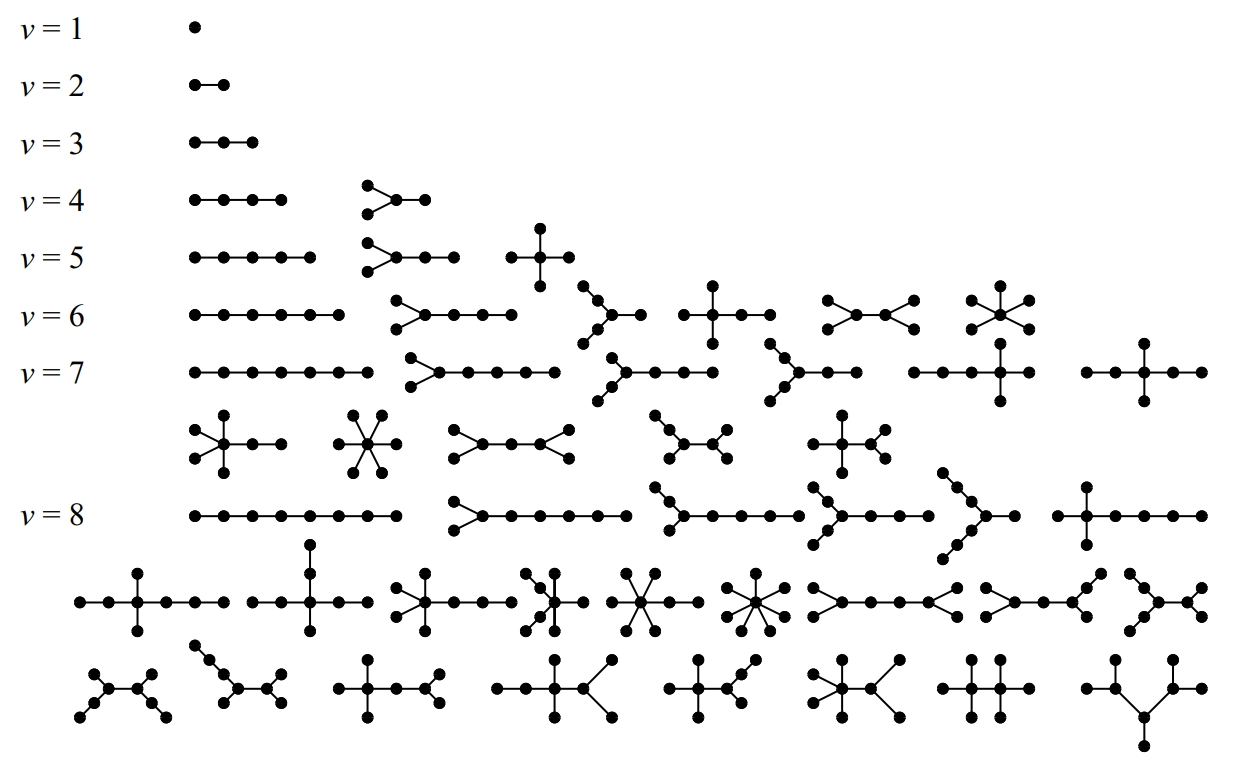
Tots els arbres amb vuit vèrtexs com a màxim
© fototeca.cat
Matemàtiques
Graf connex i acíclic (sense circuits).
Un arbre té només un vèrtex, anomenat arrel sense predecessor en el sentit de les fletxes, mentre que tot altre vèrtex té, cada un, un únic predecessor Tots els vèrtexs tenen un nombre variable de successors, que ordinariàment hom suposa ordenats per exemple, d’esquerra a dreta i de vegades són anomenats branques En la representació habitual d’un arbre l’arrel se situa al capdamunt i els arcs se suposen recorreguts en sentit descendent Els arbres han passat d’ésser un cas particular de graf a rebre un tractament matemàtic específic Són particularment útils en la modelització de …
Aleksandr Jacovlevič Khinčin
Matemàtiques
Matemàtic rus.
Estudià a la Universitat de Moscou 1911-16, d’on fou professor el 1927 Amb Kolmogorov és considerat com un dels fundadors de l’escola de Moscou, que ha fet aportacions cabdals en teoria de les probabilitats Estudià també amb NLuzin la teoria de funcions, les teories de les fraccions contínues, generalitzà la integral de Denjoy i establí la teoria general dels processos aleatoris estacionaris
Andrej Andrejevič Markov
Matemàtiques
Matemàtic rus, deixeble de P.L. Čebyšev.
Fou un dels membres més destacats de l’escola de matemàtics russos dedicats a l’estudi de la teoria de probabilitats Treballà especialment en la llei dels grans nombres, i analitzà els processos estocàstics, els quals considerà com una cadena de proves, que ha estat anomenada cadena de Markov Aplicà els seus coneixements matemàtics a la lingüística anàlisi de Markov per a estudiar la freqüència dels mots i de llurs encadenaments
Jevgenij Slutskij
Economia
Matemàtiques
Economista i matemàtic rus.
Inicià la seva formació com a matemàtic a Kíev i enginyer a Munic s’interessà posteriorment per l’economia política i el dret Collaborà amb l’Institut Central de Meteorologia 1931-34 i des del 1934 amb l’Institut Matemàtic de l’Acadèmia de Ciències de l’URSS L’obra per la qual és més conegut és l’article sobre la teoria del comportament del consumidor 1915, en el qual estableix les relacions existents entre els preus, la renda i el consum i, en especial, la juxtaposició de l’efecte renda i l’efecte substitució, ocasionada per la modificació del preu d’un bé Aquesta acció…
George Boole
Lògica
Matemàtiques
Matemàtic i lògic anglès.
Autodidacte, s’introduí en matemàtica mitjançant l’estudi de les obres de Lagrange i les de Laplace, i el 1849 obtingué una càtedra al Queen's College de Corcaigh Féu importants treballs en anàlisi matemàtica i contribuí a la fixació del llavors naixent concepte d’invariància Però la seva aportació més important fou l’inici de la lògica simbòlica És autor de The Mathematical Analysis of Logic 1847, The Calculus of Logic 1848 i de la seva obra mestra, An Investigation into the Laws of Thought, on which are Founded the Mathematical Theories of Logic and Probabilities 1854 El seu treball, que…
probabilitat
Matemàtiques
Concepte que permet d’expressar quantitativament el caràcter aleatori d’un esdeveniment o fenomen que hom creu que pot succeir.
El càlcul de probabilitats , branca de la matemàtica que presenta un gran nombre d’aplicacions científiques i tècniques, sorgí a França al s XVII amb els matemàtics B Pascal i P Fermat La motivació principal era l’estudi del guany esperat en els jocs d’atzar ruletes, daus, cartes, etc i, per tant, l’objectiu era el càlcul directe de la probabilitat utilitzant tècniques de combinatòria La noció de probabilitat en què hom es basava fou formulada l’any 1795 pel matemàtic francès P S Laplace de la següent manera “Si un fenomen pot produir un nombre de resultats diferents i igualment probables,…
aleatorietat
Matemàtiques
Propietat de les variables aleatòries de poder prendre qualsevol valor del seu condomini en tractar-se de processos en què intervé l’atzar.