Resultats de la cerca
Es mostren 16 resultats
equació quadràtica
Matemàtiques
Equació de segon grau ax2 + bx + c = 0, o, en forma reduïda, x2 + px + q = 0.
Una equació quadràtica pura és la de la forma ax 2 + b = 0 En ax 2 + bx + c = 0, la fórmula de la solució és la quantitat b 2 - 4ac és anomenada discriminant
fracció periòdica
Matemàtiques
Fracció l’expressió decimal de la qual conté una xifra o grup de xifres (anomenades període) que es repeteixen indefinidament.
P ex, el període d’1/3 = 0,333 és 3, el d’1/6 = 0,1666 és 6 Quan el període comença a les dècimes, la fracció és anomenada periòdica pura en la resta de casos és anomenada periòdica mixta
Luigi Cremona
Matemàtiques
Matemàtic italià.
Enginyer civil i arquitecte 1853, fou catedràtic de geometria superior a la Universitat de Bolonya 1860 i director de l’escola d’enginyers de Roma 1873 Senador, ocupà el ministeri d’instrucció pública 1898 Fou l’impulsor de la geometria pura a Itàlia Entre les seves obres cal remarcar Elementi di geometria projettiva 1873 i Elementi di calcolo grafico 1874
Marie-Joseph Kampé de Fériet
Matemàtiques
Matemàtica francesa.
Contribuí a crear i desenvolupar moltes de les branques de la matemàtica pura i aplicada Foren transcendents les seves aportacions a la mecànica de fluids, anàlisi, probabilitat, teoria de les equacions funcionals, teoria generalitzada de la informació, etc Fou investida doctora honoris causa a les universitats de Gant i Bolonya, i nomenada membre de les acadèmies de ciències de París, Madrid, Varsòvia, Washington i Nova York
Pierre-Ossian Bonnet
Matemàtiques
Matemàtic francès.
Fou catedràtic d’astronomia matemàtica a la Sorbona des del 1878, i membre de l’Académie des Sciences 1862 Féu treballs d’investigació en els camps de la mecànica, del càlcul infinitesimal, i, especialment, en geometria pura sobre la teoria de superfícies És autor de les memòries La théorie générale des surfaces 1845 i Mémoire sur l’emploi d’un nouveau système de coordonnées dans l’étude des propriétés des surfaces courbes , publicades al “Journal des Mathématiques”
Francesco Brioschi
Matemàtiques
Matemàtic italià.
Fou professor de geodèsia, mecànica racional i càlcul infinitesimal a la Universitat de Pavia 1852 El 1863 fou encarregat d’organitzar i dirigir la cració de l’Institut Politècnic de Milà, del qual fou director, i hi ensenya hidràulica i mecànica racional Dirigí els “Annali di Matematica Pura e Applicata” 1867-77 i fou secretari del ministeri d’instrucció pública Els seus treballs més importants desenvolupen la teoria dels invariants, i introduí a Itàlia l’obra de Karl Gustav Jacobi i de Cailey en La teoria dei determinanti e le sue applicazioni 1854, les funcions ellíptiques,…
Johannes von Neumann
Matemàtiques
Matemàtic hongarès naturalitzat nord-americà.
Fou un dels pocs matemàtics moderns que reeixí alhora en l’estudi de qüestions de teoria pura teoria de conjunts continuant les investigacions de Zermelo, àlgebra topològica, teoria dels jocs anomenats estratègics , formulació axiomàtica de la mecànica quàntica, etc i en la matemàtica aplicada calculadors electrònics amb “memòria” contenint no sols les dades numèriques d’un problema, sinó també les instruccions que permeten de resoldre'l, com l’EDVAC del 1945, i especialment les màquines autoreproductores, que imiten procediments naturals apresos de la genètica, ideades l’any…
funció exponencial
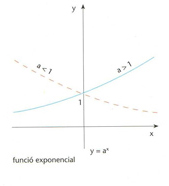
Funció exponencial
© Fototeca.cat
Matemàtiques
Funció contínua f
:ℝ→ℝ +
-{0} que satisfà f
( x
+ x
’) = f
( x
) f
( x
’), per a tot parell x,x
’∈ℝ, i f
(1)= a
, essent a
un nombre real concret que la caracteritza, anomenat base
.
És denotada per l’assignació x → a x És la funció inversa de la funció logarítmica de base Hom empra, especialment, la funció exponencial que té per base el nombre e aquesta és la inversa de la funció logarítmica neperiana ln e x = e l n x = x Quan hom no especifica la base, hom parla de funció exponencial o simplement d’exponencial, tot sobreentenent que es tracta de la funció exponencial de base e , i la nota e x o exp x Té la propietat d e x / dx = e x , i admet el desenvolupament en sèrie Aquesta sèrie convergeix també en el cos ℂ, la qual cosa permet de definir-hi la funció…
Abraham De Moivre
Matemàtiques
Matemàtic anglès d’origen francès.
Estudià a les universitats de Sedan, Saumur i París Després de la revocació de l’edicte de Nantes es traslladà a Anglaterra per tal de fugir de la persecució desencadenada a França contra els hugonots Ja a Anglaterra, l’astrònom EHalley presentà el seu treball “Specimen” 1967 a la Royal Society, de la qual fou elegit membre dos anys més tard La majoria dels seus treballs foren publicats en les Philosophical Transactions Arran de la polèmica entre Newton i Leibniz sobre la invenció del càlcul, formà part de la comissió que estudià el problema El seu primer estudi sobre probabilitat, De…
sistema binari
Matemàtiques
Electrònica i informàtica
Sistema de numeració de base dos.
En aquest sistema hom només necessita dos signes que representin els nombres zero i u Qualsevol nombre natural pot ésser descompost en suma de potències de 2, i el nombre resta determinat dient quines potències entren en la descomposició indicades amb el coeficient 0 o 1 Així, el nombre 45 = 2 5 + 2 3 + 2 2 + 2 0 és escrit, en sistema binari , 101101 dos Per a passar un nombre donat en el sistema binari al sistema decimal cal tenir en compte que cada unitat en val dues de l’ordre immediat inferior Així, el nombre 1010111 dos és Hom pot també representar, en el sistema binari, els nombres…