Resultats de la cerca
Es mostren 462 resultats
univers
Matemàtiques
Conjunt de referència els subconjunts del qual són utilitzats en un raonament concret.
En els diagrames de Venn-Euler hom sol representar l’univers amb un rectangle, dins el qual són dibuixats els diagrames dels conjunts que hom vol representar Així, en l’estudi dels conjunts de nombres reals l’univers és ℝ
espai topològic
Matemàtiques
Conjunt X en el qual s’ha donat una topologia
.
Els conjunts de la família donada són anomenats oberts , i llurs complementaris, tancats Rep el nom d' entorn obert d’un punt tot conjunt obert que el conté Base de l’espai topològic és una família de conjunts oberts que per reunió poden donar qualsevol altre obert Alguns espais topològics tenen llur topologia definida per mitjà d’una distància, la qual determina la base d’oberts de la topologia formada per les boles o esferes En són exemples la recta real ℝ i els espais euclidians de dimensions superiors ℝ n Un subespai d’un espai topològic és una part de l’espai amb la…
perspectiva cònica
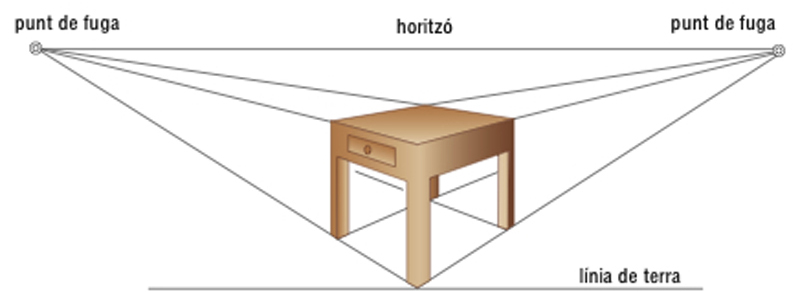
Representació d’una taula en perspectiva cònica obliqua (dos punts de fuga)
© Fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Perspectiva central el centre de projecció o pol de la qual és l’ull de l’observador.
Per al traçat d’aquesta perspectiva, hom admet que la llum que arriba a l’ull procedent de qualsevol punt d’un objecte és una línia recta, que rep el nom de raig visual Els principals elements per al seu traçat són la posició de l’ull o punt de vista , de la qual depèn l’efecte de la perspectiva l' horitzó o la línia horitzontal traçada en el pla del quadre, a l’alçada del punt de vista, que ocupa en el quadre la mateixa posició que la perspectiva de l’horitzó natural el pla geometral , que és el pla perpendicular al pla del quadre i on hom suposa que són situats l’observador i…
transformació integral
Matemàtiques
Operació mitjançant la qual una funció f(x) és transformada en una altra funció F(y) gràcies a relacions de tipus integral.
L’exemple més senzill és la simple integració F y = ∫ a y f x dx Una expressió vàlida per a un nombre important de transformacions integrals és F y = ∫ a b K x,y f x dx en la qual K x,y rep el nom de nucli i caracteritza l’esmentada transformació en molts casos, els límits d’integració són 0, ∞ i -∞, ∞ Cal esmentar, com a exemples importants, la integral ponderada, la integral de convolució, la transformada de Fourier anàlisi de Fourier, la de Laplace, la de Kankel, i la de Mellin
cargol de Pascal
Matemàtiques
Corba plana, tancada i simètrica respecte a l’eix X, l’equació de la qual és, en coordenades polars, r = 2a cosφ + K.
Presenta tres formes, segons que sigui 0 < K < 2 a cargol hiperbòlic , amb un llaç d’origen, K > 2 a > 0 cargol ellíptic , en el qual ha desaparegut el llaç a causa de l’existència d’un punt conjugat o K = 2 a cardioide El cargol de Pascal és una concoide d’una circumferència respecte a un dels seus punts Fou descrit per Étienne Pascal, pare de Blaise Pascal
axioma de Zermelo
Matemàtiques
Axioma segons el qual, donada una col·lecció de conjunts, existeix un ‘‘mètode’’ de designar un element particular de cada conjunt com un element ‘‘especial’’ d’aquest conjunt.
Aquest axioma, anomenat també axioma de l’elecció , és equivalent al teorema de Zermelo, segons el qual tot conjunt admet una relació d’ordre que en fa un conjunt ben ordenat Hi ha una versió més dèbil de l’axioma de l’elecció en el cas d’ésser finita la collecció de conjunts
sèrie de Renard
Matemàtiques
Sèrie formada pels termes d’una progressió geomètrica compresos entre 1 i 10, la raó de la qual és
, n essent, generalment, 5, 10, 20 o 40.
La més corrent és l’obtinguda amb n = 10, amb la qual cosa la raó val =1,26 Els termes d’aquesta sèrie són 1 1,25 1,6 2 2,5 3,15 4,5 6,3 8 10 Aquesta sèrie, ideada el 1879 per l’enginyer Charles Renard Damblaim 1847 — Meudon 1905, té aplicació en diversos camps industrials
rombòedre
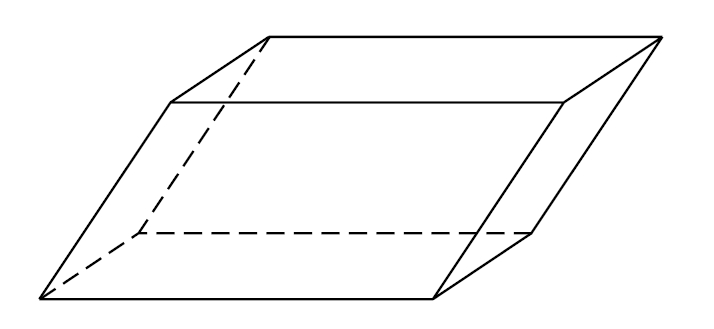
Rombòedre
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina