Resultats de la cerca
Es mostren 9 resultats
recíproca
Matemàtiques
Donada una quantitat a, la quantitat 1/a
.
És anomenada també inversa Les quantitats a i 1/ a són anomenades quantitats recíproques o inverses i llur producte és igual a 1
imatge recíproca d’un element respecte a una aplicació
Matemàtiques
Donat un element y de la imatge d’una aplicació f, conjunt format pels elements x del recorregut de f tals que f(x) = y
.
recíproc | recíproca
Matemàtiques
Donada una correspondència (G,A,B), dit de la correspondència (G-1,B,A).
recíproc | recíproca
Matemàtiques
Donat un graf G, dit del graf G-1 format pels parells ordenats (y,x) tals que (x,y) ∈G.
recíproc | recíproca
Matemàtiques
Donada una aplicació f bijectiva, dit de l’aplicació f-1 definida per f-1(x) = y ⇔f(y) = x.
semigrup
Matemàtiques
Conjunt on hi ha definida una operació interna que és associativa.
Tot grup és semigrup, però la recíproca no és certa Un semigrup és anomenat també monoide
espiral d’Arquimedes
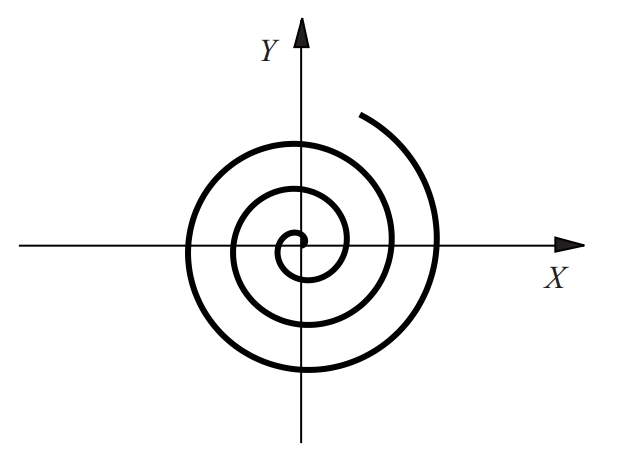
espiral d’Arquimedes (m = 1)
© fototeca.cat
Matemàtiques
Corba plana transcendent d’equació polar rm = kmθ.
En el cas de l’espiral clàssica d’Arquimedes, m = 1, però també són espirals d’Arquimedes l’espiral de Fermat, on m = 2, i l’espiral hiperbòlica o recíproca, on m = -1
mitjana
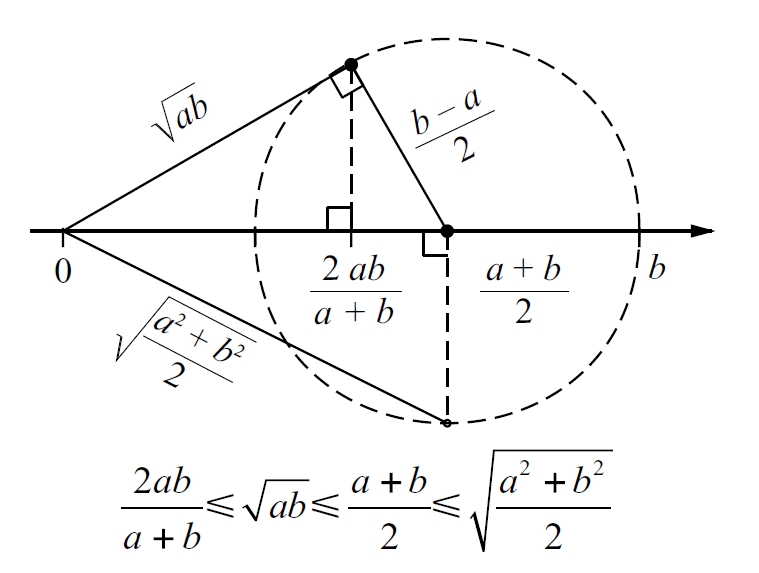
Mitjanes dels nombres a i b: harmònica, geomètrica, aritmètica i quadràtica
© fototeca.cat
Matemàtiques
Donats n valors o observacions x1, x2, ..., xn, valor x definit com la suma de tots ells dividida per llur nombre, és a dir, .
La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població , mentre que si les observacions són d’una mostra aleatòria de la població mostreig, x és la mitjana de la mostra A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n 1 , n 2 , , n k i freqüències respectives f 1 , f 2 , , f k , la fórmula per al càlcul de la mitjana és…
relació
Matemàtiques
Lligam entre diversos elements d’un conjunt.
Per tal de precisar aquesta idea intuïtiva, hom defineix la relació com a qualsevol subconjunt d’un producte cartesià del conjunt amb ell mateix és a dir, que els elements són relacionats si formen un element del subconjunt En general, en una relació intervé un nombre determinat d’elements n així, una relació d’ordre entre els elements és un subconjunt del producte de n conjunts A El tipus de relació més freqüent és aquella en què n = 2, anomenada relació binària , que és un subconjunt de A × A Si els dos elements són a i b , hom diu que a R b , o que a és relacionat amb b —o sia, que a,b…