Resultats de la cerca
Es mostren 8 resultats
histograma
Matemàtiques
Representació gràfica, formada per rectangles, de les freqüències d’una variable.
Quan la variable pren valors discrets, tots els rectangles tenen la mateixa amplada i llur altura és proporcional a la freqüència corresponent al punt on el rectangle és situat Quan la variable és contínua, els rectangles són contigus i l’àrea de cadascun d’ells, que té per base un cert interval de la variable, és proporcional al valor global de la freqüència corresponent a l’interval
paral·lelogram
Matemàtiques
Quadrilàter que té els costats oposats paral·lels i, per tant, iguals.
Les diagonals d’un parallelogram es tallen en llur punt mitjà, anomenat centre del parallelogram Si un parallelogram té els quatre costats iguals, és anomenat rombe Si els quatre costats són perpendiculars, és anomenat rectangle Els parallelograms que són rombes i rectangles alhora són anomenats quadrats , i els que no són ni rombes ni rectangles, romboides L’àrea d’un parallelogram resulta de multiplicar la longitud d’un costat, que hom anomena base , per la distància que el separa del seu parallel, anomenada altura
paral·lelepípede
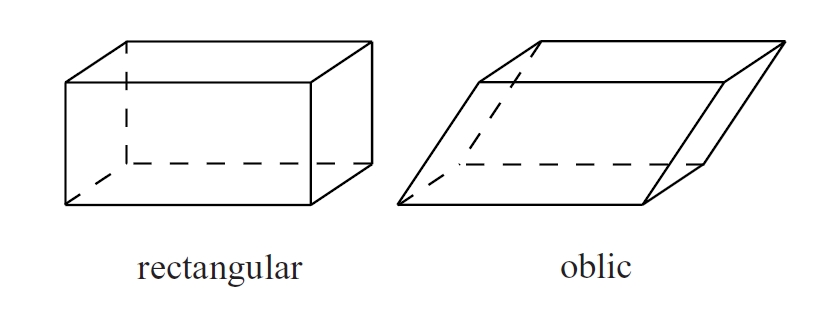
Paral·lelepípede
Matemàtiques
Prisma de sis cares, totes elles paral·lelograms.
Quan el prisma és recte i totes les cares són rectangles, és anomenat ortòedre L’ hexàedre és l’únic parallelepípede que és políedre regular
Muḥammad ibn Ahmad ibn Muḥammad ibn al-Lait
Astronomia
Matemàtiques
Astrònom i matemàtic andalusí.
Adscrit a la cort de Muǧāhid de Dénia, d’entre la seva vasta producció sobresurt Respostes a preguntes sobre matemàtiques d’al-Biruni i Sobre propietats dels triangles rectangles escalens
número d’or
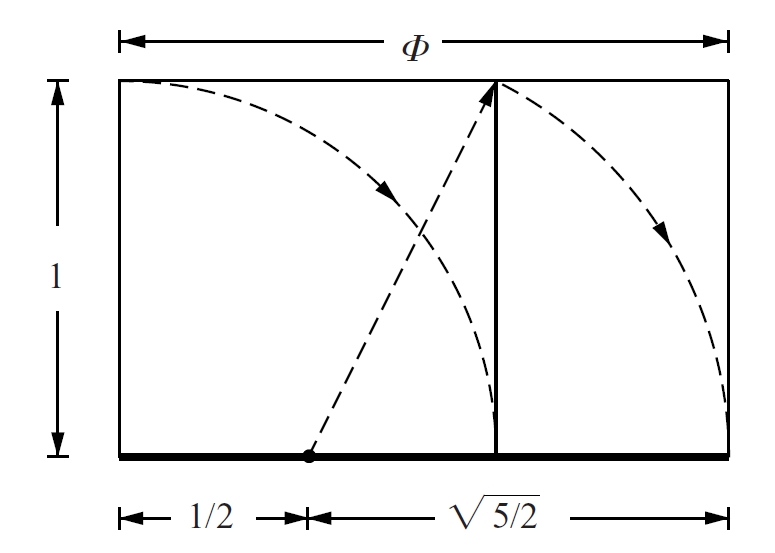
número d’or
Matemàtiques
Nombre irracional algebraic positiu que, elevat al quadrat, és igual a ell mateix més una unitat: (1 + ⎷5 ) ⁄ 2 = 1,618.
El número d’or apareix en molts problemes geomètrics relatius a les divisions harmòniques de segments o a proporcions de rectangles, o entre mides Així, un rectangle té de proporció el número d’or si, i solament si, té la mateixa proporció del rectangle que resulta de treure del rectangle original un quadrat Aquest nombre és el límit dels quocients 1 ⁄ 1, 2 ⁄ 1, 3 ⁄ 2, 5 ⁄ 3 dels termes de la successió de Fibonacci i té una important presència en elements naturals i artístics, especialment en pintura i arquitectura, ja que que el número d’or és igual al cosinus de 36º i, per tant…
freqüència
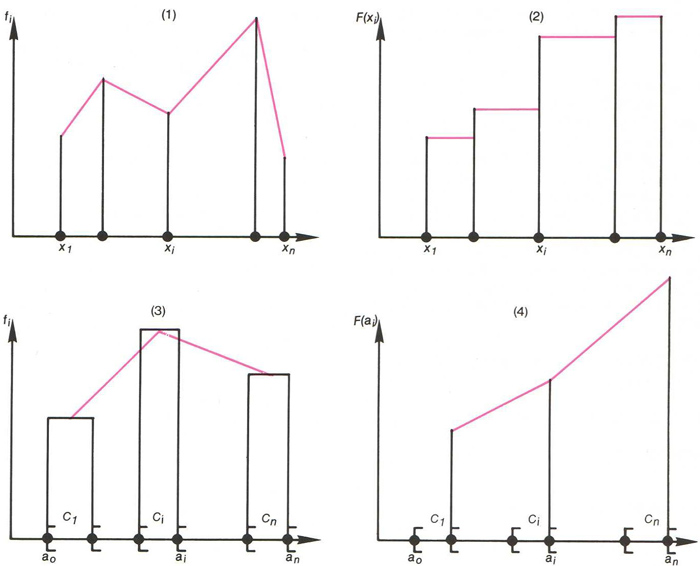
Representacions gràfiques de la freqüència d’una distribució estadística: si el caràcter quantitatiu és discret, (1) és el seu polígon de freqüencies i (2) és la seva corba cumulativa; si el caràcter quantitatiu és continu, (3) és el seu polígon de freqüències i (4) és la seva corba cumulativa
© Fototeca.cat
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, quocient entre l’efectiu d’un valor concret del caràcter, o d’una classe de valors, i el nombre d’individus que integren la mostra.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,,x n sobre una mostra de N individus, la freqüència o freqüència relativa del valor x i és el quocient f i = n i / N , on n i és l’ efectiu del valor x i és a dir, el nombre d’individus de la mostra que presenten el valor x i del caràcter La representació gràfica de la funció de distribució x i → f i és una línia poligonal obtinguda en unir els punts de coordenades x i , f i , i =1,, n , anomenada polígon de freqüències Si el caràcter quantitatiu és continu , donada una classe o interval C i = a i - 1 , a i del conjunt de…
mesura
Matemàtiques
Aplicació m definida entre una àlgebra de conjunts ɑ d’un espai mesurable (Ω, ɑ) i el conjunt ℝ+ dels nombres reals positius.
L’aplicació compleix que la mesura de la unió de dos conjunts A i B de ɑ és igual a la suma de les respectives mesures, és a dir ∀ A ∈ ɑ i ∀ B ∈ ɑ tals que A ∩ B = ∅, m A + m B La terna Ω, ɑ, m és anomenada espai de mesura , i els conjunts de l’àlgebra ɑ són anomenats mesurables En el cas que ɑ sigui una σ-àlgebra de Borel, una mesura m és anomenada σ-additiva si la mesura d’una unió infinita i numerable de conjunts de ɑ disjunts dos a dos és igual a la suma de les respectives mesures, és a dir essent A i ∈ ɑ i A i ∩ A j = ∅, per a tot i, j tals que i ≠ j Una mesura és anomenada fitada…
geometria
Matemàtiques
Part de la matemàtica basada en la intuïció d’espai.
El nom prové de la seva primera aplicació la mesura de la Terra Els diversos apartats en què hom divideix la geometria fan referència a la natura dels objectes d’estudi i al mètode emprat Per a una definició unitària de la geometria elemental, l’any 1872 CF Klein proposà,en el “programa d’Erlangen”,la noció de geometria com a consideració d’un espai el conjunt dels punts i un grup de transformacions d’aquest espai, els invariants del qual serien les nocions de la geometria en qüestió El primer estudi de la geometria fou de caràcter intuïtiu, i consistí en la compilació de fets relatius a…