Resultats de la cerca
Es mostren 4 resultats
espiral
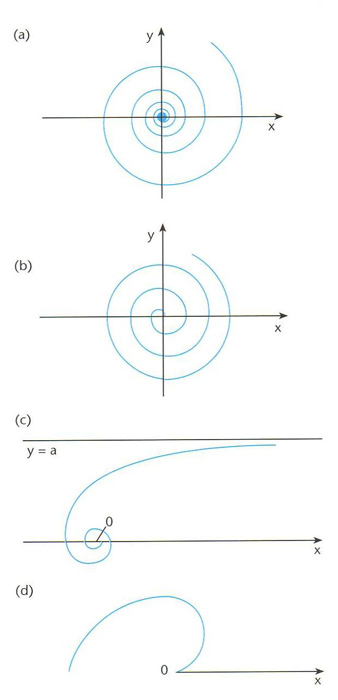
espiral: (a) logarítmica; (b) d’Arquímedes; (c) hiperbòlica; (d) parabòlica
© fototeca.cat
Matemàtiques
Corba plana descrita per un punt que gira al voltant d’un punt fix allunyant-se contínuament segons una llei determinada, característica per a cada tipus d’espiral.
Analíticament són representades gairebé sempre en coordenades polars Les equacions de les espirals més importants són espiral logarítmica o equiangular, r = e aθ espiral d’Arquimedes , r = r o /2πθ espiral hiperbòlica, r θ = a /θ espiral parabòlica o de Fermat, r 2 = a θ, i espiral sinusoidal, r n = a n sin n θ
lemniscata de Bernoulli
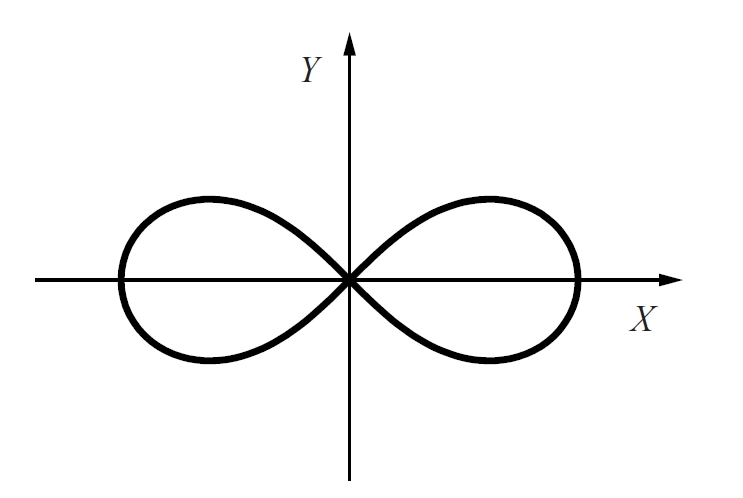
lemniscata de Bernoulli
Matemàtiques
Espiral sinusoïdal d’equació cartesiana (x2 + y2)2 = a2(x2 - y2).
És la inversa d’una hipèrbola equilàtera respecte del seu origen
anàlisi de Fourier
Física
Matemàtiques
Estudi de les funcions que té per finalitat d’expressar-les mitjançant una sèrie o una integral en què intervenen les funcions trigonomètriques.
El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier Tota funció periòdica f x , contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera la sèrie que apareix en aquesta expressió és la sèrie de Fourier de o associada a la funció f x El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació o freqüència angular de f , és a dir, ω=2π/ T , on T és el període de f El primer terme de la sèrie de Fourier de f , terme que correspon al…