Resultats de la cerca
Es mostren 63 resultats
solució
Matemàtiques
Cadascuna de les quantitats que satisfan les condicions d’un problema, especialment d’una equació.
problema dels set ponts de Königsberg
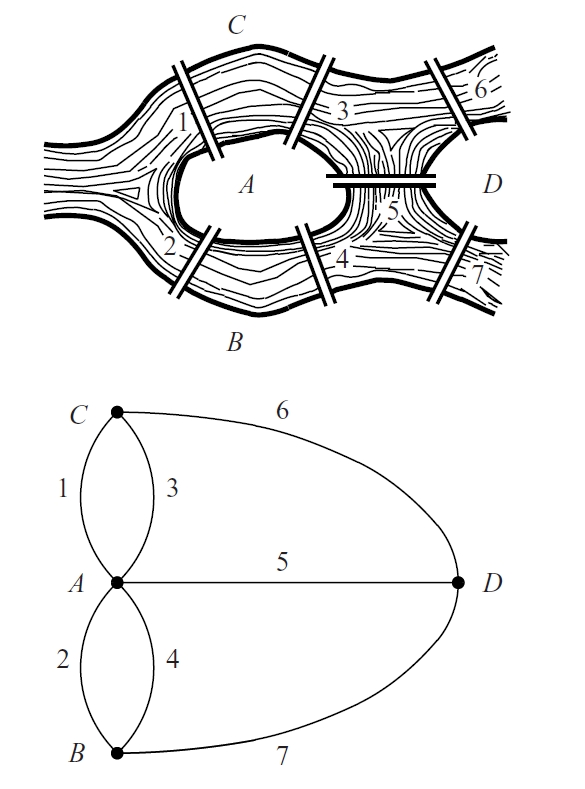
problema dels set ponts de Königsberg
Fototeca.cat
Matemàtiques
Problema la solució del qual s’associa sovint amb l’origen de la teoria de grafs.
La ciutat prussiana de Königsberg actualment Kaliningrad està dividida pel riu Pregol’a, que voreja l’illa de Kneiphof Hi havia set ponts disposats com s’indica a la figura Els habitants de la ciutat es plantejaven si era possible fer un recorregut tancat que passés una sola vegada per cadascun dels set ponts En llenguatge de teoria de grafs, la pregunta és si el graf és eulerià La resposta és negativa La solució del problema va ser trobada per Leonard Euler, el 1736, introduint per primer cop la noció de graf i resolent a la vegada un problema de caràcter més general
condicions inicials
Física
Matemàtiques
Donada una equació diferencial, condicions que cal imposar a la solució general per tal que prengui, ella i les seves derivades, uns determinats valors per a un valor especificat de la variable independent.
Les condicions inicials permeten, doncs, de determinar la solució particular del problema en ajustar les constants arbitràries de la solució general Per exemple, en el problema del moviment d’una massa puntual, un cop conegudes les forces que hi actuen, el moviment concret que realitza depèn només de la posició i la velocitat en un instant inicial, x t o i v t o , essent aquestes les condicions inicials del problema
investigació operativa
Matemàtiques
Branca de les matemàtiques molt lligada a l’estadística i a l’anàlisi dels processos d’optimització, consistent a aplicar tècniques matemàtiques i estadístiques a la solució de problemes governamentals, empresarials, industrials, educatius, etc.
Les tècniques de la investigació operativa són particularment útils en l’equilibrament d’objectius conflictius amb un gran nombre de línies d’acció alternatives, amb conflictes d’interessos i amb un gran nombre de variables complexes i interaccionants La investigació operativa s’utilitza per a conduir i coordinar les operacions o les activitats dins un sistema organitzat empresa, administració pública, etc, i els estudis que en són el resultat intenten proporcionar a l’executiu una base sòlida, científica i quantitativa per a la presa de decisions Es caracteritza també per l’aplicació del…
regla de Ruffini
Matemàtiques
Mètode per a comprovar, donats un polinomi p(x) i un valor a, si aquest valor és solució de l’equació p(x) = 0, és a dir, si x - a divideix el polinomi p(x).
El mètode dóna, a més, el polinomi p x / x-a , i així, d’una forma successiva, hom pot arribar per reiteració a determinar totes les solucions reals del polinomi És, però, un mètode de comprovació i no pas un algorisme de resolució El mètode és el següent sigui, per exemple, el polinomi x 2 + x - 2 hom escriu els coeficients 1, 1, -2, i a continuació, suposat un valor qualsevol escollit entre els divisors del coeficient independent que en aquest cas és -2, per exemple 1, hom fa els càlculs següents És a dir, el primer coeficient resta igual al segon hom suma el producte del primer coeficient…
condicions de contorn
Física
Matemàtiques
Donada una equació diferencial, condicions que cal imposar a la solució general per tal que prengui uns determinats valors en punts o zones concrets del domini de valors de la variable independent, zones anomenades contorns del problema.
Per exemple, el potencial electroestàtic d’una distribució de càrregues elèctriques ha de satisfer l’equació diferencial de Laplace ∇ 2 V =0 amb la condició de contorn que V sigui constant sobre la superfície dels conductors que hi hagi a l’espai del problema Les condicions de contorn són imposades per les lleis físiques, per la simetria o per la disposició experimental del problema Si el problema dinàmic és controlat per una o diverses equacions diferencials en derivades parcials, la solució particular del problema generalment ha de satisfer, a més d’unes condicions de contorn,…
singular
Matemàtiques
Dit de la solució d’una equació diferencial que no és deduïble de l’anomenada solució general
.
equació de Riccati
Matemàtiques
Equació diferencial de la forma y´ = dy/dx = f1(x) + y f2(x) + y2 f3(x).
No té una solució general calculable per quadratures, però si hom en coneix una solució particular y 0 , aleshores és fàcil de trobar-ne la solució general Fent el canvi y = y 0 + z , resulta l' equació de Bernoulli z´ = z f 2 x + 2 f 3 x y 0 + z 2 f 3 x , i fent el nou canvi u = 1/ z , hom n'obté una equació diferencial lineal d’integració immediata
sistema d’equacions lineals
Matemàtiques
Conjunt d’equacions lineals de les quals interessen les solucions comunes.
Un sistema d’aquest tipus és anomenat compatible si admet solució, i incompatible en el cas contrari Un sistema compatible és determinat si la solució és única, i indeterminat si, per contra, hi ha infinites solucions Els sistemes d’equacions lineals són anomenats no homogenis si els termes independents b 1 , b m no són tots nuls, i homogenis en el cas contrari La regla de Cramer permet, mitjançant l’ús dels determinants, de resoldre els sistemes de 3 equacions amb 3 incògnites té solució on és el determinant del sistema, que ha d’ésser no nul
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Pàgina següent
- Última pàgina